《六年級數(shù)學(xué)上冊教案- 8 數(shù)學(xué)廣角——數(shù)與形 人教新課標(biāo) (1)》由會員分享，可在線閱讀，更多相關(guān)《六年級數(shù)學(xué)上冊教案- 8 數(shù)學(xué)廣角——數(shù)與形 人教新課標(biāo) (1)（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

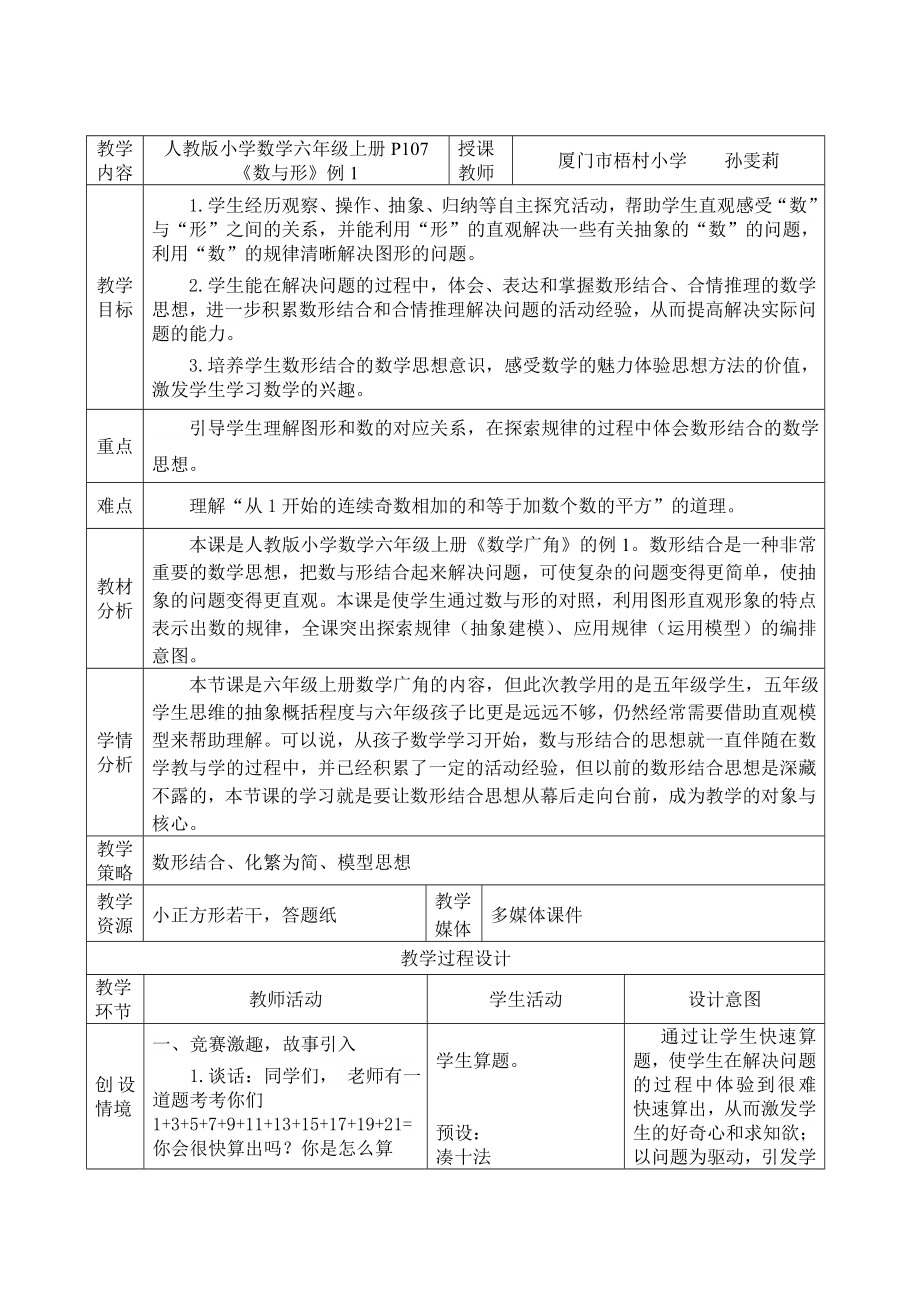
1、 人教版 學(xué)科 年級 冊教案 教學(xué)內(nèi)容 人教版小學(xué)數(shù)學(xué)六年級上冊P107 《數(shù)與形》例1 授課 教師 廈門市梧村小學(xué) 孫雯莉 教學(xué)目標(biāo) 1. 學(xué)生經(jīng)歷觀察、操作、抽象、歸納等自主探究活動，幫助學(xué)生直觀感受“數(shù)”與“形”之間的關(guān)系，并能利用“形”的直觀解決一些有關(guān)抽象的“數(shù)”的問題，利用“數(shù)”的規(guī)律清晰解決圖形的問題。 2. 學(xué)生能在解決問題的過程中，體會、表達和掌握數(shù)形結(jié)合、合情推理的數(shù)學(xué)思想，進一步積累數(shù)形結(jié)合和合情推理解決問題的活動經(jīng)

2、驗，從而提高解決實際問題的能力。 3. 培養(yǎng)學(xué)生數(shù)形結(jié)合的數(shù)學(xué)思想意識，感受數(shù)學(xué)的魅力體驗思想方法的價值，激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣。 重點 引導(dǎo)學(xué)生理解圖形和數(shù)的對應(yīng)關(guān)系，在探索規(guī)律的過程中體會數(shù)形結(jié)合的數(shù)學(xué)思想。 難點 理解“從1開始的連續(xù)奇數(shù)相加的和等于加數(shù)個數(shù)的平方”的道理。 教材分析 本課是人教版小學(xué)數(shù)學(xué)六年級上冊《數(shù)學(xué)廣角》的例1。數(shù)形結(jié)合是一種非常重要的數(shù)學(xué)思想，把數(shù)與形結(jié)合起來解決問題，可使復(fù)雜的問題變得更簡單，使抽象的問題變得更直觀。本課是使學(xué)生通過數(shù)與形的對照，利用圖形直觀形象的特點表示出數(shù)的規(guī)律，全課突出探索規(guī)律（抽象建模）、應(yīng)用規(guī)律（運

3、用模型）的編排意圖。 學(xué)情分析 本節(jié)課是六年級上冊數(shù)學(xué)廣角的內(nèi)容，但此次教學(xué)用的是五年級學(xué)生，五年級學(xué)生思維的抽象概括程度與六年級孩子比更是遠(yuǎn)遠(yuǎn)不夠，仍然經(jīng)常需要借助直觀模型來幫助理解?？梢哉f，從孩子數(shù)學(xué)學(xué)習(xí)開始，數(shù)與形結(jié)合的思想就一直伴隨在數(shù)學(xué)教與學(xué)的過程中，并已經(jīng)積累了一定的活動經(jīng)驗，但以前的數(shù)形結(jié)合思想是深藏不露的，本節(jié)課的學(xué)習(xí)就是要讓數(shù)形結(jié)合思想從幕后走向臺前，成為教學(xué)的對象與核心。 教學(xué)策略 數(shù)形結(jié)合、化繁為簡、模型思想 教學(xué)資源 小正方形若干，答題紙 教學(xué) 媒體 多媒體課件 教學(xué)過程設(shè)計 教學(xué) 環(huán)節(jié) 教師活動 學(xué)生活動 設(shè)計意圖 創(chuàng)

4、設(shè)情境 一、競賽激趣，故事引入 1.談話：同學(xué)們， 老師有一道題考考你們1+3+5+7+9+11+13+15+17+19+21=你會很快算出嗎？你是怎么算的？ 2. 教師說古希臘數(shù)學(xué)家畢達哥拉斯海灘上擺石子發(fā)現(xiàn)計算規(guī)律的故事。 3. 觀察算式中加數(shù)的特點。 4.猜數(shù)學(xué)家是怎么擺石子的？猜數(shù)學(xué)家把這些小石子擺成什么圖形？ 師：這么多數(shù)相加,你猜猜看數(shù)學(xué)家是怎么擺小石子的？ 板書： 1 1+3=4 1+3+5=9 1+3+5+7=16 師：那么你們再猜猜科學(xué)家會把這些小石子擺成什么形狀才能發(fā)現(xiàn)這種特殊的計算方法呢？ 學(xué)生算題。

5、 預(yù)設(shè)： 湊十法 預(yù)設(shè)： 1. 都是奇數(shù) 2. 每兩個數(shù)都相差2 3. 都是連續(xù)奇數(shù) 預(yù)設(shè)：那也就是說先擺1個小石子，然后在1個小石子的基礎(chǔ)上再擺3個，總共擺4個；接著…… 預(yù)設(shè)：三角形、正方形、長方形 通過讓學(xué)生快速算題，使學(xué)生在解決問題的過程中體驗到很難快速算出，從而激發(fā)學(xué)生的好奇心和求知欲；以問題為驅(qū)動，引發(fā)學(xué)生積極思考、動手探究、合作交流。 通過故事激發(fā)學(xué)生探索欲望。 通過這一系列活動，滲透這列數(shù)的特點和所拼擺的圖形的形狀對于研究特殊的計算方法是很有幫助的。

6、 第一環(huán)節(jié)：以形助數(shù)，建立模型 1. 初擺圖形 （1）咱們手上沒有石子，怎么辦？ （2）用正方形拼擺圖形。 師：用正方形來代替小石子好嗎？接下來就請同學(xué)們試著擺一擺，邊擺邊觀察、邊思考，看看從你擺的圖形當(dāng)中是否能發(fā)現(xiàn)這種特殊的計算方法是什么。 （3）反饋：你有什么發(fā)現(xiàn)嗎？ A.展示學(xué)生擺的圖形。 B.觀察擺成正方形的圖，集中觀察1+3=4，這個4還可以怎么算？ 師：怎么想的？ 師：是的，擺成的這個正方形可以看做每行2個，有兩行，這個2在這個算式中還可表示有（2個加數(shù)）。 2.再擺圖形 師：1+3這兩個加數(shù)相加能擺出這樣特殊的正方形，得出2×2，那么1+3+5

7、呢，1+3+5+7呢能不能也擺出這樣特殊的正方形，也寫成幾乘幾呢？（稍加停頓，讓學(xué)生思考）請剛才沒有擺出正方形的同學(xué)也重新擺一擺，并說說你的發(fā)現(xiàn)。 反饋。 師：其他小組也有這樣的發(fā)現(xiàn)嗎？再請一組同學(xué)上來邊擺邊說。 預(yù)設(shè)：用別的東西代替 學(xué)生擺圖形 生匯報 預(yù)設(shè)：展示長方形、正方形、三角形的圖形 預(yù)設(shè)：2*2 預(yù)設(shè)：擺成的大正方形當(dāng)中每行2個，有2行，所以可以用2*2表示。 生擺圖形 預(yù)設(shè)：1+3+5能擺成正方形，每行3個，有3行，結(jié)果能用3×3表示；1+3+5+7

8、也能擺成正方形，每行4個，有4行，結(jié)果可用4×4表示。 滲透符號化思想 讓學(xué)生試著 第二環(huán)節(jié)：尋找規(guī)律，抽象建模 1.引導(dǎo)觀察，初建模型 師：1+3=4這兩個加數(shù)相加能寫成2×2,簡寫為2的平方，1+3+5這3個加數(shù)相加能寫成3×3，簡寫為3的平方，1+3+5+7能寫成4×4，簡寫為4的平方，那么如果是1+3+5+7+9你能很快算出來嗎？你怎么想的？（結(jié)合課件演示）還有不同的想法嗎？你有沒有什么發(fā)現(xiàn)？ 師：所以你認(rèn)為這類題的解法是？ 2.不斷完善，建立模型 師：這真是一個了不起的發(fā)現(xiàn)。 誒，孫老師怎么寫了個問號呢？

9、難道這句話有什么問題？ 3.小結(jié)規(guī)律 預(yù)設(shè)：可以寫成5的平方。 （1）因為這個算式能擺成5行，每行5個。 （2）因為2個數(shù)相加是2的平方、3個數(shù)相加是3的平方…… 預(yù)設(shè)：幾個數(shù)相加結(jié)果就是幾的平方。 預(yù)設(shè)：不完整。還必須是從1開始，連續(xù)奇數(shù)相加。 利用數(shù)形結(jié)合，讓學(xué)生有理有據(jù)的闡述發(fā)現(xiàn)的規(guī)律，抽象出數(shù)學(xué)模型。 讓學(xué)生在不斷的辨析中明確是從1開始連續(xù)奇數(shù)相加結(jié)果就是幾的平方。 第三環(huán)節(jié)：運用模型，解決問題 1. 計算大數(shù)據(jù)題目。（那么剛開始這道題你能怎樣很快算出？） 1+3+5+7+9+11+1

10、3+15+17+19+21 你怎么想的？ 2. 課堂練習(xí) （1） =92 （2）1+3+5+7+5+3+1= （3）3+5+7+9+11+13+15= 3.小結(jié)：現(xiàn)在不但是從1開始連續(xù)幾個奇數(shù)相加同學(xué)們能算得很快，有些變化的題，同學(xué)們也能靈活的計算。說明咱們找到的方法巧妙確實巧妙！ 咱們剛才是通過哪些途徑方法找到規(guī)律的？ 是的，很多時候一些數(shù)或者算式要發(fā)現(xiàn)其規(guī)律并不那么容易，但我們可以利用拼擺圖形，借助圖形的直觀來幫助我們發(fā)現(xiàn)或理解這些隱藏的規(guī)律。這是為什么呢？（因為圖形比較直觀）所以我們經(jīng)常借助圖形來探索規(guī)律。這就是今天我們學(xué)習(xí)的“數(shù)與形”

11、（板書：數(shù)與形） 學(xué)生獨立完成，并交流反饋。 生列式 預(yù)設(shè)：找規(guī)律、擺圖形 運用模型，解決大數(shù)據(jù)問題。 通過小結(jié)引導(dǎo)學(xué)生明白數(shù)學(xué)的學(xué)習(xí)經(jīng)常要通過圖形的直觀來幫助理解和解決問題。 第四環(huán)節(jié)：運用方法，課外延伸 談話：數(shù)的計算可以借助圖形來思考，那么圖形中會不會也蘊藏著數(shù)的規(guī)律呢？（課件出示108頁做一做第2題。） 留給同學(xué)們回家思考，下節(jié)課交流。 學(xué)生在剛才學(xué)習(xí)的基礎(chǔ)上，學(xué)會自己發(fā)現(xiàn)模型，建立模型，運用模型。 總結(jié)回顧 最后老師帶來了華羅庚爺爺?shù)囊皇自姡簲?shù)缺形時少直觀，形少數(shù)時難入微，數(shù)形結(jié)合百般好，隔離分家萬事休。（課件演示） 師：是的，數(shù)與形的結(jié)合是多么的奇妙，未來還有許多的知識等待著我們?nèi)ヌ剿鳌? 5