《2020高考數(shù)學(xué) 核心考點(diǎn) 第2講 數(shù)形結(jié)合思想復(fù)習(xí)（無答案）》由會員分享，可在線閱讀，更多相關(guān)《2020高考數(shù)學(xué) 核心考點(diǎn) 第2講 數(shù)形結(jié)合思想復(fù)習(xí)（無答案）（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

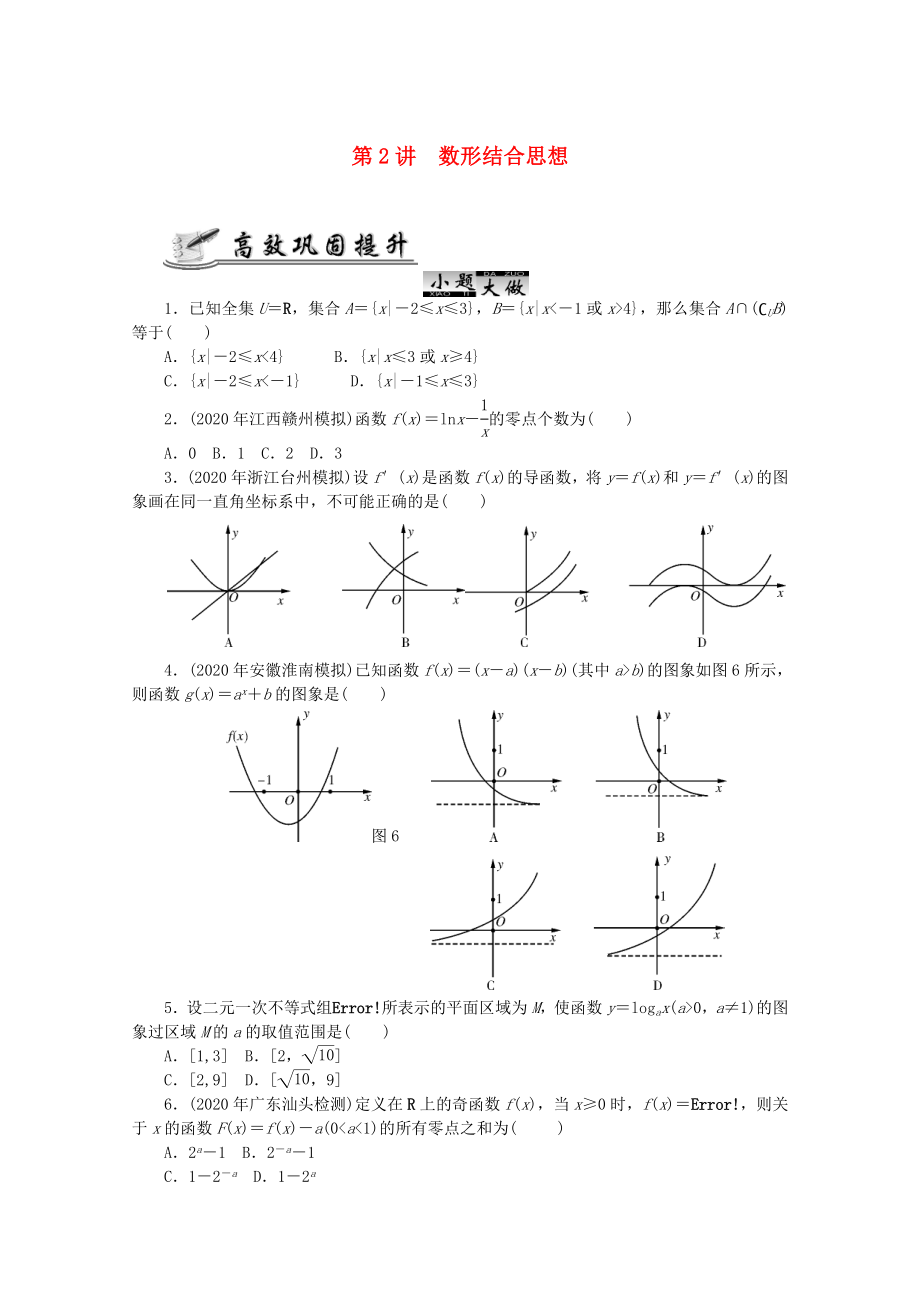
1、第2講　數(shù)形結(jié)合思想 1．已知全集U＝R，集合A＝{x|－2≤x≤3}，B＝{x|x<－1或x>4}，那么集合A∩(?UB)等于(　　) A．{x|－2≤x<4}　　 B．{x|x≤3或x≥4} C．{x|－2≤x<－1}　　 D．{x|－1≤x≤3} 2．(2020年江西贛州模擬)函數(shù)f(x)＝lnx－的零點(diǎn)個數(shù)為(　　) A．0 B．1 C．2 D．3 3．(2020年浙江臺州模擬)設(shè)f′(x)是函數(shù)f(x)的導(dǎo)函數(shù)，將y＝f(x)和y＝f′(x)的圖象畫在同一直角坐標(biāo)系中，不可能正確的是(　　) 4．(2020年安徽淮南模擬)已知函數(shù)f(x)＝(x

2、－a)(x－b)(其中a>b)的圖象如圖6所示，則函數(shù)g(x)＝ax＋b的圖象是(　　) 圖6 5．設(shè)二元一次不等式組所表示的平面區(qū)域?yàn)镸，使函數(shù)y＝logax(a>0，a≠1)的圖象過區(qū)域M的a的取值范圍是(　　) A．[1,3] B．[2，] C．[2,9] D．[，9] 6．(2020年廣東汕頭檢測)定義在R上的奇函數(shù)f(x)，當(dāng)x≥0時，f(x)＝，則關(guān)于x的函數(shù)F(x)＝f(x)－a(0

3、－m與曲線y＝有兩個不同的交點(diǎn)，則實(shí)數(shù)m的取值范圍是__________． 8. 已知f(x)是以2為周期的偶函數(shù)，當(dāng)x∈[0,1]時，f(x)＝x，且在[－1,3]內(nèi)關(guān)于x的方程f(x)＝kx＋k＋1(k∈R，k≠－1)有四個根，則k得取值范圍是____________． 9．已知A(1,1)為橢圓＋＝1內(nèi)一點(diǎn)，F(xiàn)1為橢圓左焦點(diǎn)，P為橢圓上一動點(diǎn)．求|PF1|＋|PA|的最大值和最小值． 10．(2020年安徽模擬)已知函數(shù)f(x)＝ax3＋bx2＋cx在x＝±1處取得極值，且在x＝0處的切線的斜率為－3. (1)求f(x)的解析式； (2)若過點(diǎn)A(2，m)可作曲線y＝f(x)的三條切線，求實(shí)數(shù)m的取值范圍．