《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 課后限時集訓(xùn)41 簡單幾何體的表面積與體積 文（含解析）北師大版》由會員分享，可在線閱讀，更多相關(guān)《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 課后限時集訓(xùn)41 簡單幾何體的表面積與體積 文（含解析）北師大版（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

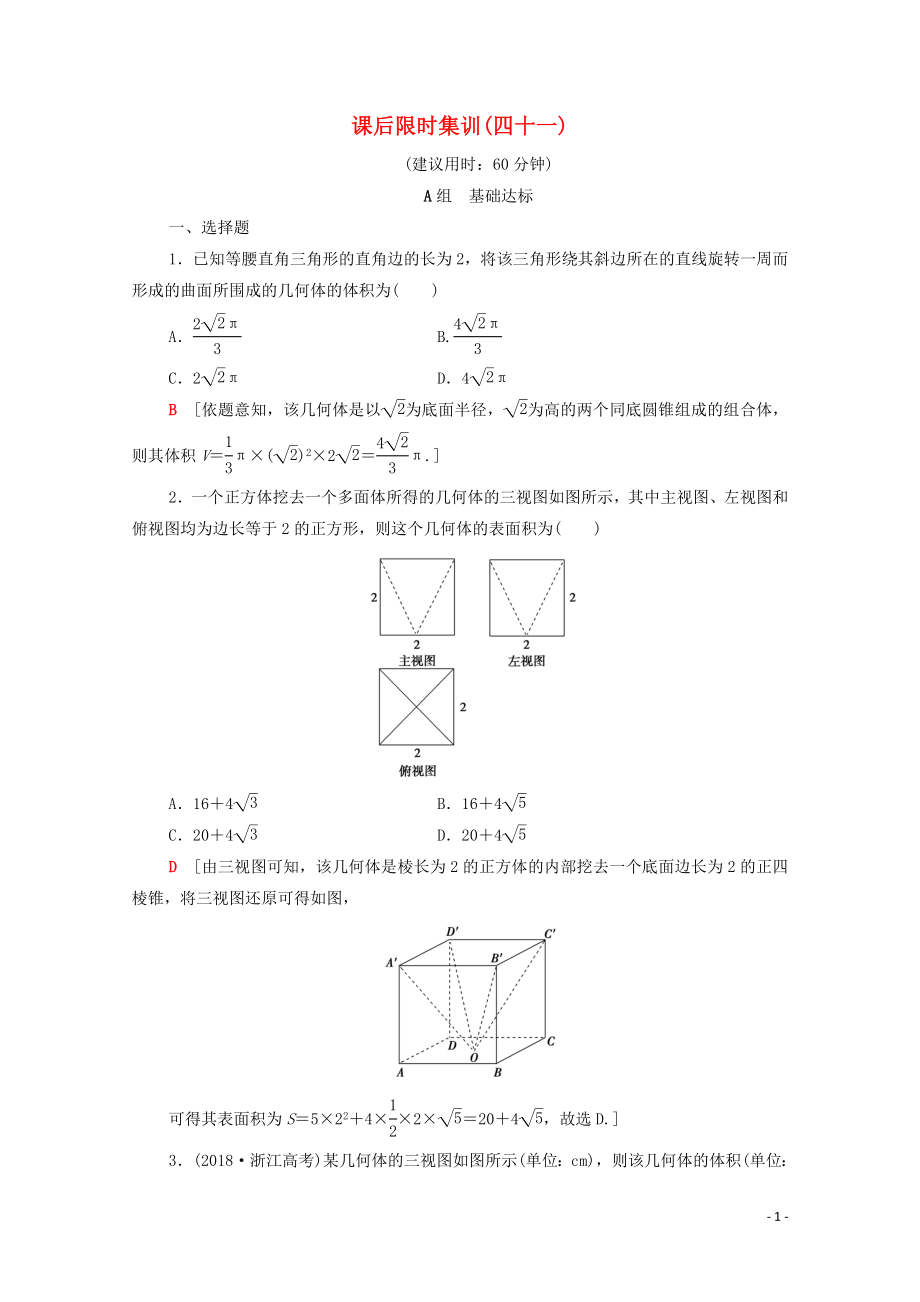
1、課后限時集訓(xùn)(四十一)　 (建議用時：60分鐘) A組　基礎(chǔ)達(dá)標(biāo) 一、選擇題 1．已知等腰直角三角形的直角邊的長為2，將該三角形繞其斜邊所在的直線旋轉(zhuǎn)一周而形成的曲面所圍成的幾何體的體積為(　　) A．　　　 B. C．2π D．4π B　[依題意知，該幾何體是以為底面半徑，為高的兩個同底圓錐組成的組合體，則其體積V＝π×()2×2＝π.] 2．一個正方體挖去一個多面體所得的幾何體的三視圖如圖所示，其中主視圖、左視圖和俯視圖均為邊長等于2的正方形，則這個幾何體的表面積為(　　) A．16＋4 B．16＋4 C．20＋4 D．20＋4 D　[由三視圖可知，該幾何體是棱長

2、為2的正方體的內(nèi)部挖去一個底面邊長為2的正四棱錐，將三視圖還原可得如圖， 可得其表面積為S＝5×22＋4××2×＝20＋4，故選D.] 3．(2018·浙江高考)某幾何體的三視圖如圖所示(單位：cm)，則該幾何體的體積(單位：cm3)是(　　) A．2　　　　B．4 C．6　　　　D．8 C　[由三視圖可知，該幾何體是一個底面為直角梯形的直四棱柱，所以該幾何體的體積V＝×(1＋2)×2×2＝6.故選C．] 4．某幾何體的三視圖如圖所示，且該幾何體的體積是3，則主視圖中的x的值是(　　) A．2 B． C． D．3 D　[由三視圖知，該幾何體是四棱錐，底面是直角梯形

3、，且S底＝×(1＋2)×2＝3， ∴V＝x·3＝3，解得x＝3.] 5．(2019·昆明模擬)一個幾何體的三視圖如圖所示，則該幾何體的外接球的表面積為(　　) A．36π B．8π C．π D．π B　[根據(jù)幾何體的三視圖，得該幾何體是底面為等腰直角三角形，高為2的直三棱錐，如圖所示， 則該直三棱錐的外接球是對應(yīng)直三棱柱的外接球，設(shè)幾何體外接球的半徑為R，∴2R＝VB. ∵VB＝＝2，∴R＝， ∴該幾何體的外接球的表面積是4πR2＝8π.故選B.] 二、填空題 6．現(xiàn)有橡皮泥制作的底面半徑為5，高為4的圓錐和底面半徑為2，高為8的圓柱各一個，若將它們重新制作成總體積

4、與高均保持不變，但底面半徑相同的新的圓錐和圓柱各一個，則新的底面半徑為______． 　[設(shè)新的底面半徑為r，由題意得 ×π×52×4＋π×22×8＝×π×r2×4＋π×r2×8， ∴r2＝7，∴r＝.] 7．一個六棱錐的體積為2，其底面是邊長為2的正六邊形，側(cè)棱長都相等，則該六棱錐的側(cè)面積為________． 12　[設(shè)正六棱錐的高為h，棱錐的斜高為h′. 由題意，得×6××2××h＝2， ∴h＝1，∴斜高h(yuǎn)′＝＝2， ∴S側(cè)＝6××2×2＝12.] 8．(2019·惠州模擬)已知三棱錐S-ABC，△ABC是直角三角形，其斜邊AB＝8，SC⊥平面ABC，SC＝6，則三棱錐S

5、-ABC的外接球的表面積為________． 100π　[將三棱錐S-ABC放在長方體中(圖略)，易知三棱錐S-ABC所在長方體的外接球，即為三棱錐S-ABC的外接球，所以三棱錐S-ABC的外接球的直徑2R＝＝10，即三棱錐S -ABC的外接球的半徑R＝5，所以三棱錐S-ABC的外接球的表面積S＝4πR2＝100π.] 三、解答題 9．如圖，從正方體ABCD-A1B1C1D1的8個頂點中選出的4個點恰為一個正四面體的頂點． (1)若選出4個頂點包含點A，請在圖中畫出這個正四面體； (2)求棱長為a的正四面體外接球的半徑． [解]　(1)如圖所示，選取的四個點分別為A，D1，B1

6、，C． (2)棱長為a的正四面體外接球的半徑等于正方體外接球的半徑等于正方體對角線長的一半，因為正四面體的棱長a，所以正方體的邊長為a，因此外接球的半徑為×a＝a. 10．(2015·全國卷Ⅱ)如圖，長方體ABCD-A1B1C1D1中，AB＝16，BC＝10，AA1＝8，點E，F(xiàn)分別在A1B1，D1C1上，A1E＝D1F＝4.過點E，F(xiàn)的平面α與此長方體的面相交，交線圍成一個正方形． (1)在圖中畫出這個正方形(不必說明畫法和理由)； (2)求平面α把該長方體分成的兩部分體積的比值． [解]　(1)交線圍成的正方形EHGF如圖所示． (2)如圖，作EM⊥AB，垂足為M，

7、則AM＝A1E＝4，EB1＝12，EM＝AA1＝8. 因為四邊形EHGF為正方形，所以EH＝EF＝BC＝10. 于是MH＝＝6，AH＝10，HB＝6. 故S四邊形A1EHA＝×(4＋10)×8＝56， S四邊形EB1BH＝×(12＋6)×8＝72. 因為長方體被平面α分成兩個高為10的直棱柱， 所以其體積的比值為. B組　能力提升 1．(2019·青島模擬)如圖為某個幾何體的三視圖，則該幾何體的體積為(　　) A．12－　　　　　B．12－π C．12－ D．12－ A　[由三視圖可知，該幾何體是由一個正四棱柱挖掉一個半圓錐所得到的幾何體，其直觀圖如圖所示，其中正

8、四棱柱的底面正方形的邊長a＝2，半圓錐的底面半徑r＝1，高h(yuǎn)＝3，所以正四棱柱的體積V1＝a2h＝22×3＝12，半圓錐的體積V2＝×r2h＝×12×3＝，所以該幾何體的體積V＝V1－V2＝12－.] 2．(2018·株洲模擬)已知正三棱錐P-ABC的主視圖和俯視圖如圖所示，則此三棱錐外接球的表面積為(　　) A． B． C． D．12π B　[如圖，作PG⊥CB于點G，連接AG，設(shè)點P在底面ABC內(nèi)的射影為D，連接PD，依題易得AB＝2，PG＝，PA＝4，AD＝2，PD＝2，PD⊥平面ABC．易知，正三棱錐P-ABC外接球的球心在PD上，不妨設(shè)球心為O，半徑為r，連接OA，則

9、在Rt△AOD中，r2＝22＋(2－r)2?r2＝，S＝4πr2＝.故選B.] 3．(2018·全國卷Ⅱ)已知圓錐的頂點為S，母線SA，SB互相垂直，SA與圓錐底面所成角為30°.若△SAB的面積為8，則該圓錐的體積為________． 8π　[由題意畫出圖形，如圖，設(shè)AC是底面圓O的直徑，連接SO，則SO是圓錐的高．設(shè)圓錐的母線長為l，則由SA⊥SB，△SAB的面積為8，得l2＝8，得l＝4.在Rt△ASO中，由題意知∠SAO＝30°，所以SO＝l＝2，AO＝l＝2.故該圓錐的體積V＝π×AO2×SO＝π×(2)2×2＝8π.] 4．一個透明的球形裝飾品內(nèi)放置了兩個公共底面的圓錐，且這

10、兩個圓錐的頂點和底面圓周都在這個球面上，如圖，已知圓錐底面面積是這個球面面積的，設(shè)球的半徑為R，圓錐底面半徑為r. (1)試確定R與r的關(guān)系，并求出較大圓錐與較小圓錐的體積之比； (2)求出兩個圓錐的體積之和與球的體積之比． [解]　(1)不妨設(shè)球的半徑為4； 則球的表面積為64π，圓錐的底面積為12π， 所以圓錐的底面半徑為2. 由幾何體的特征知球心到圓錐底面的距離，球的半徑以及圓錐底面的半徑三者可以構(gòu)成一個直角三角形． 由此可以求得球心到圓錐底面的距離是＝2， 所以圓錐體積較小者的高為4－2＝2， 同理可得圓錐體積較大者的高為4＋2＝6. 又由這兩個圓錐的底面相同， 所以較大圓錐與較小圓錐的體積之比等于它們高之比，即3∶1. (2)由(1)可得兩個圓錐的體積和為·π·(2)2·8＝32π，球的體積為·π·43＝π， 故兩個圓錐的體積之和與球的體積之比為32π∶π＝3∶8. - 8 -