《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 第六篇 不等式 第3節(jié) 二元一次不等式(組)與簡(jiǎn)單的線性規(guī)劃問(wèn)題課時(shí)作業(yè) 文（含解析）新人教A版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2020版高考數(shù)學(xué)一輪復(fù)習(xí) 第六篇 不等式 第3節(jié) 二元一次不等式(組)與簡(jiǎn)單的線性規(guī)劃問(wèn)題課時(shí)作業(yè) 文（含解析）新人教A版（9頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

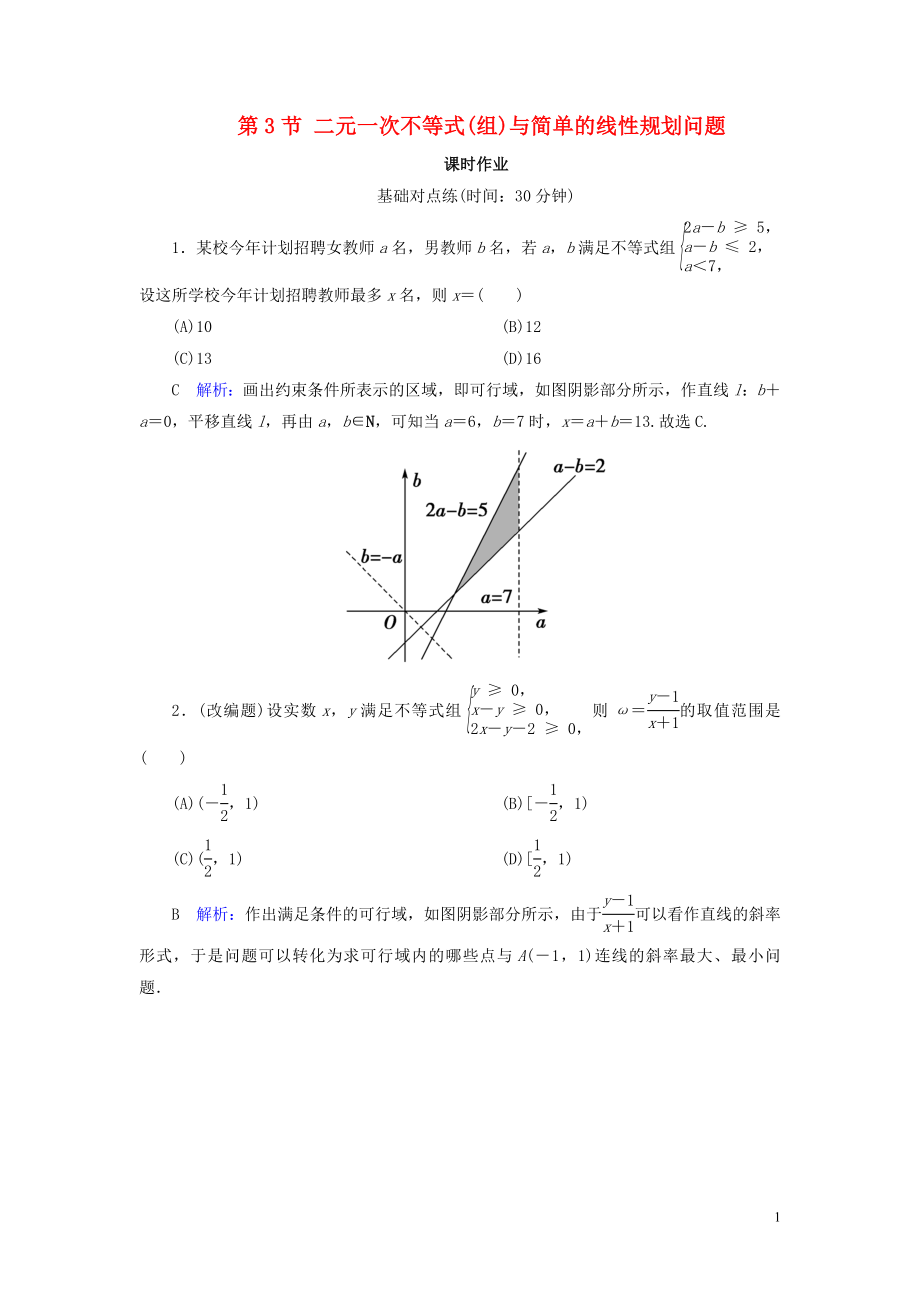
1、第3節(jié) 二元一次不等式(組)與簡(jiǎn)單的線性規(guī)劃問(wèn)題 課時(shí)作業(yè) 基礎(chǔ)對(duì)點(diǎn)練(時(shí)間：30分鐘) 1．某校今年計(jì)劃招聘女教師a名，男教師b名，若a，b滿足不等式組設(shè)這所學(xué)校今年計(jì)劃招聘教師最多x名，則x＝(　　) (A)10 (B)12 (C)13 (D)16 C　解析：畫(huà)出約束條件所表示的區(qū)域，即可行域，如圖陰影部分所示，作直線l：b＋a＝0，平移直線l，再由a，b∈N，可知當(dāng)a＝6，b＝7時(shí)，x＝a＋b＝13.故選C. 2．(改編題)設(shè)實(shí)數(shù)x，y滿足不等式組則ω＝的取值范圍是(　　) (A)(－，1) (B)[－，1) (C)(，1) (D)[，1) B　解析：

2、作出滿足條件的可行域，如圖陰影部分所示，由于可以看作直線的斜率形式，于是問(wèn)題可以轉(zhuǎn)化為求可行域內(nèi)的哪些點(diǎn)與A(－1，1)連線的斜率最大、最小問(wèn)題． 如圖，當(dāng)直線y＝ωx＋ω＋1過(guò)點(diǎn)B時(shí)，斜率最小，此時(shí)ω＝kAB＝＝－； 當(dāng)直線y＝ωx＋ω＋1與x－y＝0平行時(shí)，斜率最大，此時(shí)ω＝1，但它與陰影區(qū)域無(wú)交點(diǎn)，取不到． 于是連線斜率的范圍為，即ω＝的取值范圍是. 3．已知變量x，y滿足約束條件x＋y－3≥0，2x－y－9≤0，y≤2，若使z＝ax＋y取得最小值的最優(yōu)解有無(wú)窮多個(gè)，則實(shí)數(shù)a的取值集合是(　　) (A){－2，0} (B){1，－2} (C){0，1} (D){－2，

3、0，1} B　解析：作出不等式組表示的平面區(qū)域，如圖中陰影部分所示． 由z＝ax＋y得y＝－ax＋z. 若a＝0，則直線y＝－ax＋z＝z，此時(shí)z取得最小值的最優(yōu)解只有一個(gè)，不滿足題意； 若－a>0，則直線y＝－ax＋z在y軸上的截距取得最小值時(shí)，z取得最小值，此時(shí)當(dāng)直線y＝－ax與直線2x－y－9＝0平行時(shí)滿足題意，此時(shí)－a＝2，解得a＝－2； 若－a<0，則直線y＝－ax＋z在y軸上的截距取得最小值時(shí)，z取得最小值，此時(shí)當(dāng)直線y＝－ax與直線x＋y－3＝0平行時(shí)滿足題意，此時(shí)－a＝－1，解得a＝1. 綜上可知，a＝－2或a＝1.故選B. 4．設(shè)變量x，y滿足約束條件且不等

4、式x＋2y≤14恒成立，則實(shí)數(shù)a的取值范圍是(　　) (A)[8，10] (B)[8，9] (C)[6，9] (D)[6，10] A　解析：不等式組表示的平面區(qū)域如圖中陰影部分所示，顯然a≥8，否則可行域無(wú)意義．由圖可知x＋2y在點(diǎn)(6，a－6)處取得最大值 2a－6，由2a－6≤14得，a≤10，故選A. 5．某公司生產(chǎn)甲、乙兩種桶裝產(chǎn)品．已知生產(chǎn)甲產(chǎn)品1桶需耗A原料1千克、B原料2千克；生產(chǎn)乙產(chǎn)品1桶需耗A原料2千克，B原料1千克．每桶甲產(chǎn)品的利潤(rùn)是300元，每桶乙產(chǎn)品的利潤(rùn)是400元．公司在生產(chǎn)這兩種產(chǎn)品的計(jì)劃中，要求每天消耗A、B原料都不超過(guò)12千克．通過(guò)合理安排

5、生產(chǎn)計(jì)劃，從每天生產(chǎn)的甲、乙兩種產(chǎn)品中，公司共可獲得的最大利潤(rùn)是(　　) (A)1 800元 (B)2 400元 (C)2 800元 (D)3 100元 C　解析：設(shè)生產(chǎn)甲產(chǎn)品x桶，乙產(chǎn)品y桶，每天利潤(rùn)為z元， 則z＝300x＋400y. 作出可行域，如圖陰影部分所示．作直線300x＋400y＝0，向右上平移，過(guò)點(diǎn)A時(shí)，z＝300x＋400y取最大值，由 得∴A(4，4)，∴zmax＝300×4＋400×4＝2 800.故選C. 6．如果點(diǎn)P在平面區(qū)域上，點(diǎn)Q在曲線x2＋(y＋2)2＝1上．那么|PQ|的最小值為(　　) (A) (B)－1 (C)2－1

6、(D)－1 A　解析：如圖，當(dāng)P取點(diǎn)，Q取點(diǎn)(0，－1)時(shí)，|PQ|的最小值為.故選A. 7．設(shè)x，y滿足約束條件若z＝的最小值為，則a的值為_(kāi)_______． 解析：∵＝1＋，而表示過(guò)點(diǎn)(x，y)與(－1，－1)連線的斜率，易知a＞0，∴可作出可行域，知的最小值是，即＝＝＝?a＝1. 答案：1 8．如圖，點(diǎn)(x，y)在四邊形ABCD內(nèi)部和邊界上運(yùn)動(dòng)，那么2x－y的最小值為_(kāi)_______． 解析：令b＝2x－y，則y＝2x－b，如圖所示，作斜率為2的平行線y＝2x－b， 當(dāng)經(jīng)過(guò)點(diǎn)A時(shí)，直線在y軸上的截距最大，為－b，此時(shí)b＝2x－y取得最小值，為b＝2×1－1＝

7、1. 答案：1 9．(2018西安期末)設(shè)x，y滿足約束條件則z＝2x－y取得最大值時(shí)的最優(yōu)解為_(kāi)_______． 解析：作可行域： Z表示目標(biāo)函數(shù)線縱截距的相反數(shù)，所以要使z最大，即縱截距最小，所以當(dāng)目標(biāo)函數(shù)線過(guò)B(5，2)時(shí)，目標(biāo)函數(shù)值最大，為2×5－2＝8. 答案：(5，2) 10．(2018永州三模)設(shè)實(shí)數(shù)x，y滿足約束條件，則z＝的最大值是________． 解析：z＝表示點(diǎn)(x，y)到(0，0)的斜率， 由可行域可知，過(guò)點(diǎn)A(2，2)時(shí)，取最大值1. 答案：1 能力提升練(時(shí)間：15分鐘) 11．(2018池州期末)實(shí)數(shù)x，y滿足，目標(biāo)函數(shù)z＝x－2y

8、的最大值為(　　) (A)1 (B)－1 (C)2 (D)－2 B　解析：畫(huà)出表示的可行域，如圖區(qū)域?yàn)殚_(kāi)放的陰影部分，可求得B(5，3)，由圖可知，函數(shù)z＝x－2y過(guò)點(diǎn)(5，3)時(shí)， zmax＝x－2y＝5－6＝－1，函數(shù)z＝x－2y的最大值為－1，故選B. 12．當(dāng)x，y滿足不等式組時(shí)，－2≤kx－y≤2恒成立，則實(shí)數(shù)k的取值范圍是(　　) (A)[－1，1] (B)[－2，0] (C)[－，] (D)[－，0] D　解析：作出不等式組表示的平面區(qū)域，如圖中陰影部分所示，設(shè)z＝kx－y，由得即B(－2，2)，由得即C(2，0)， 由得即A(－5，－1)，

9、要使不等式－2≤kx－y≤2恒成立，則即所以－≤k≤0，故選D. 13．(2018江西南昌市高三調(diào)研)若關(guān)于x、y的不等式組表示的平面區(qū)域是一個(gè)三角形，則k的取值范圍是________． 解析：不等式|x|＋|y|≤2表示的平面區(qū)域?yàn)槿鐖D所示的正方形ABCD及其內(nèi)部． 直線y＋2＝k(x＋1)過(guò)定點(diǎn)P(－1，－2)，斜率為k， 要使平面區(qū)域表示一個(gè)三角形，則KPD＜k≤kPA 或k＜kPC. 而kPD＝0，kPA＝＝， kPC＝＝－2，故0＜k≤或k＜－2. 答案：(－∞，－2)∪(0，] 14．(2018蚌埠二中)已知實(shí)數(shù)x，y滿足約束條件，則z＝x＋2y的最小值為_(kāi)

10、_______． 解析：作可行域，則直線z＝x＋2y過(guò)點(diǎn)A(2，0)時(shí)z取最小值2. 答案：2 15．(2018衡水中學(xué))已知實(shí)數(shù)x，y滿足約束條件則z＝的最大值為_(kāi)_______． 解析：作出不等式表示的平面區(qū)域(如圖示：陰影部分)： 其中C z＝＝1＋，即m＝表示可行域上的動(dòng)點(diǎn)與定點(diǎn)P(－1，2)連線的斜率， 最大值為kPC＝－ ∴y＝的最大值為1－＝ 答案： 16．咖啡館配制兩種飲料，甲種飲料每杯含奶粉9克、咖啡4克、糖3克，乙種飲料每杯含奶粉4克、咖啡5克、糖10克．已知每天原料的使用限額為奶粉3 600克、咖啡2 000克、糖3 000克，甲種飲料每杯能獲利潤(rùn)0.7元，乙種飲料每杯能獲利潤(rùn)1.2元，每天應(yīng)配制兩種飲料各多少杯能獲利最大？ 解：設(shè)每天配制甲種飲料x(chóng)杯、乙種飲料y杯可以獲得最大利潤(rùn)，利潤(rùn)總額為z元． 由條件知：z＝0.7x＋1.2y，變量x、y滿足 作出不等式組所表示的可行域如圖所示． 作直線l：0.7x＋1.2y＝0， 把直線l向右上方平移至經(jīng)過(guò)A點(diǎn)的位置時(shí)， z＝0.7x＋1.2y取最大值． 由方程組 得A點(diǎn)坐標(biāo)(200，240)． 答：應(yīng)每天配制甲種飲料200杯，乙種飲料240杯方可獲利最大． 9