《（浙江專用）2020版高考數(shù)學(xué)一輪復(fù)習(xí) 專題8 立體幾何與空間向量 第61練 立體幾何中的易錯(cuò)題練習(xí)（含解析）》由會(huì)員分享，可在線閱讀，更多相關(guān)《（浙江專用）2020版高考數(shù)學(xué)一輪復(fù)習(xí) 專題8 立體幾何與空間向量 第61練 立體幾何中的易錯(cuò)題練習(xí)（含解析）（7頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

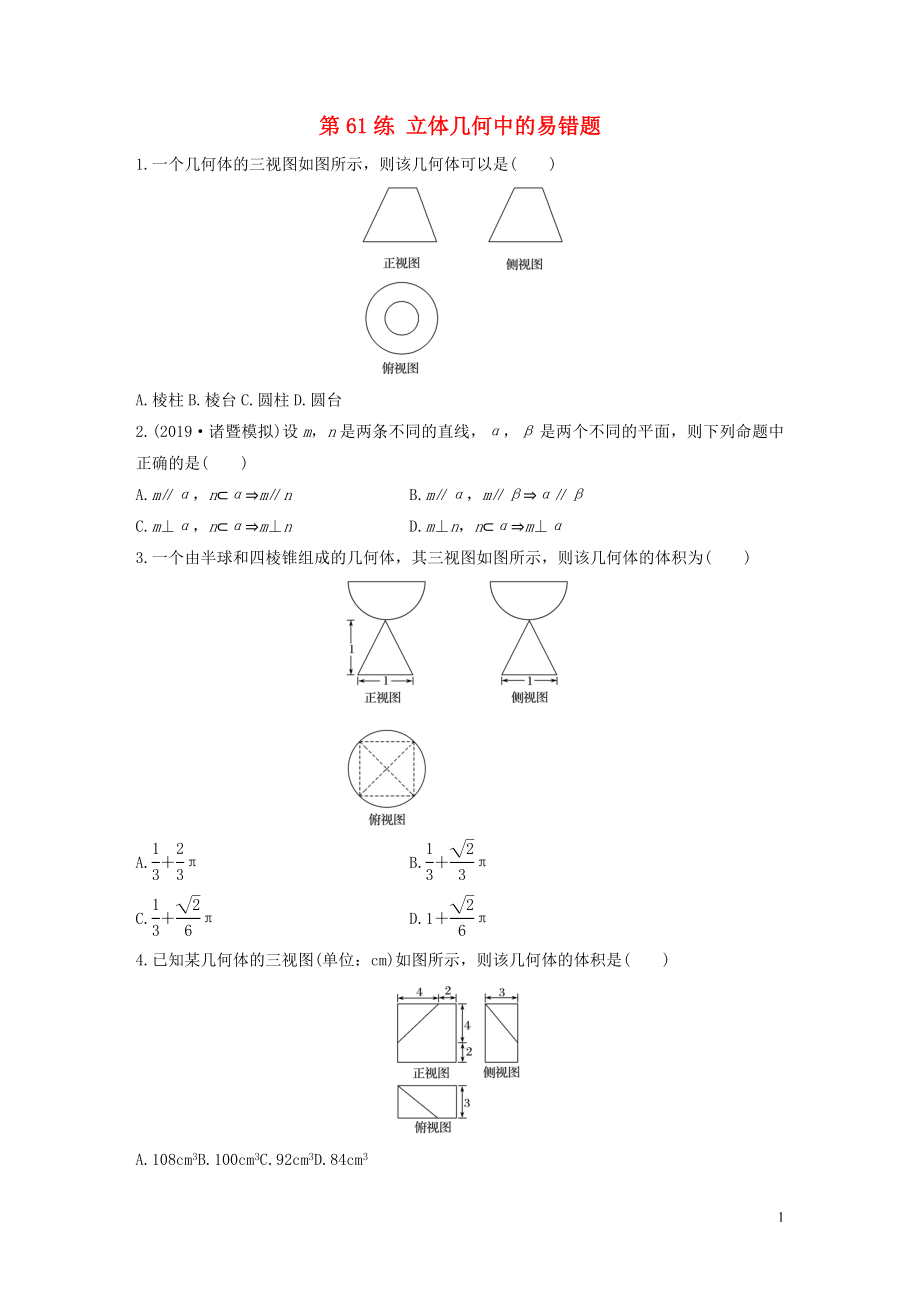
1、第61練 立體幾何中的易錯(cuò)題 1.一個(gè)幾何體的三視圖如圖所示，則該幾何體可以是(　　) A.棱柱B.棱臺(tái)C.圓柱D.圓臺(tái) 2.(2019·諸暨模擬)設(shè)m，n是兩條不同的直線，α，β是兩個(gè)不同的平面，則下列命題中正確的是(　　) A.m∥α，n?α?m∥n B.m∥α，m∥β?α∥β C.m⊥α，n?α?m⊥n D.m⊥n，n?α?m⊥α 3.一個(gè)由半球和四棱錐組成的幾何體，其三視圖如圖所示，則該幾何體的體積為(　　) A.＋π B.＋π C.＋π D.1＋π 4.已知某幾何體的三視圖(單位：cm)如圖所示，則該幾何體的體積是(　　) A.108cm3B.100c

2、m3C.92cm3D.84cm3 5.(2019·杭州模擬)已知直線m，n與平面α，β，下列命題正確的是(　　) A.m∥α，n∥β且α∥β，則m∥n B.m⊥α，n∥β且α⊥β，則m⊥n C.α∩β＝m，m⊥n且α⊥β，則n⊥α D.m⊥α，n⊥β且α⊥β，則m⊥n 6.如圖，在矩形ABCD中，E為線段DC上一動(dòng)點(diǎn)，現(xiàn)將△AED沿AE折起，使二面角D—AE—B的平面角為120°，點(diǎn)D在平面ABC上的射影為K，當(dāng)E從D′運(yùn)動(dòng)到C，則點(diǎn)K所形成的軌跡圖形為(　　) A.線段 B.一段圓弧 C.一段橢圓弧 D.一段拋物線 7.某裝飾品的三視圖如圖所示，則該裝飾品的表面積為(　

3、　) A.16＋π B.16－(－1)π C.16＋(－1)π D.20＋(－1)π 8.已知三棱錐S－ABC的所有頂點(diǎn)都在球O的球面上，△ABC是邊長為1的正三角形，SC為球O的直徑，且SC＝2，則此棱錐的體積為(　　) A.B.C.D. 9.如圖，長方體ABCD－A1B1C1D1的底面是邊長為a的正方形，若在側(cè)棱AA1上至少存在一點(diǎn)E，使得∠C1EB＝90°，則側(cè)棱AA1的長的最小值為(　　) A.a B.2a C.3a D.4a 10.(2019·衢州模擬)如圖，在長方體A1B1C1D1—A2B2C2D2中，A1A2＝2A1B1＝2B1C1，A，B，C分別是A1A

4、2，B1B2，C1C2的中點(diǎn)，記直線D2C與AD1所成的角為α，平面A2BCD2與平面ABC1D1所成二面角為β，則(　　) A.cosα＝cosβ B.sinα＝sinβ C.cosα>cosβ D.sinα

5、________. 14.(2019·紹興上虞區(qū)模擬)某幾何體的三視圖如圖所示(單位：cm)，則該幾何體的體積是________cm3，幾何體表面中最大面的面積是________cm2. 15.一個(gè)幾何體的三視圖如圖所示，則這個(gè)幾何體的外接球的半徑為________. 16.(2019·杭州模擬)如圖，在正方體ABCD—A1B1C1D1中，AB＝，P為空間中的動(dòng)點(diǎn)且AP＝1，則三棱錐C—PB1D1的體積的最大值為________. 答案精析 1．D　2.C　3.C　4.B　5.D　6.B　7.C　 8．A　[設(shè)E為△ABC的重心，連接OA，OB，OE. ∵三棱錐S

6、－ABC內(nèi)接于球O， ∴OB＝OC＝OA＝1. 又△ABC為等邊三角形， ∴OE⊥平面ABC， ∴三棱錐的高h(yuǎn)＝2OE. ∵AB＝AC＝BC＝1，E為△ABC的重心，連接CE， ∴CE＝，∴OE＝＝，∴h＝， ∴VS－ABC＝S△ABC·h ＝××1××＝.] 9．B　[設(shè)AA1＝h，AE＝x， A1E＝h－x，x∈[0，h]， 則BE2＝a2＋x2，C1E2 ＝(a)2＋(h－x)2，BC＝a2＋h2. 又∠C1EB＝90°，所以BE2＋C1E2＝BC， 即a2＋x2＋(a)2＋(h－x)2＝a2＋h2， 即關(guān)于x的方程x2－h(huán)x＋a2＝0，x∈[0，h]有解，

7、x＝0時(shí)，a2＝0，不合題意， x>0時(shí)，h＝＋x≥2a，當(dāng)且僅當(dāng)x＝a時(shí)取等號(hào)．即側(cè)棱AA1的最小值為2a.] 10．B　[由題意知α＝60°，AB2⊥平面A2BCD2，B1C⊥平面ABC1D1，則，可分別視為平面A2BCD2，平面ABC1D1的一個(gè)法向量，又因?yàn)榕c的夾角為60°，所以β＝60°或β＝120°，即sinα＝sinβ，故選B.] 11．π　12.　13.8 14.　2 解析　還原三視圖得如圖中的三棱錐D1—BCM， ＝××2×1×2＝，S△BCM＝＝1，＝D1C·BC＝2，＝×2×＝，所以表面中最大面的面積為2. 15. 解析　由已知中的三視圖可得 該幾何

8、體是平放的直三棱柱，且三棱柱的底面為直角三角形，高為12； 可還原為長、寬、高是12,8,6的長方體， 其外接球的直徑是長方體體對(duì)角線的長， ∴(2R)2＝122＋82＋62＝244， 即R2＝61，∴半徑R＝. 16. 解析　依題可知，動(dòng)點(diǎn)P的軌跡為以A為球心，1為半徑的球的球面，＝，連接AC1，易知AC1⊥平面CB1D1，求點(diǎn)A到平面CB1D1的距離h，先求點(diǎn)C1到平面CB1D1的距離h1，由＝得××××＝h1××××，所以h1＝1，故A到平面CB1D1的距離h＝AC1－1＝2，故P到平面CB1D1的距離h2的取值范圍為[1,3]，所以＝h2××××＝h2∈，故三棱錐C—PB1D1的體積的最大值為. 7