《初三數(shù)學(xué)中考復(fù)習(xí)投影與視圖專(zhuān)題復(fù)習(xí)訓(xùn)練題》由會(huì)員分享，可在線閱讀，更多相關(guān)《初三數(shù)學(xué)中考復(fù)習(xí)投影與視圖專(zhuān)題復(fù)習(xí)訓(xùn)練題（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

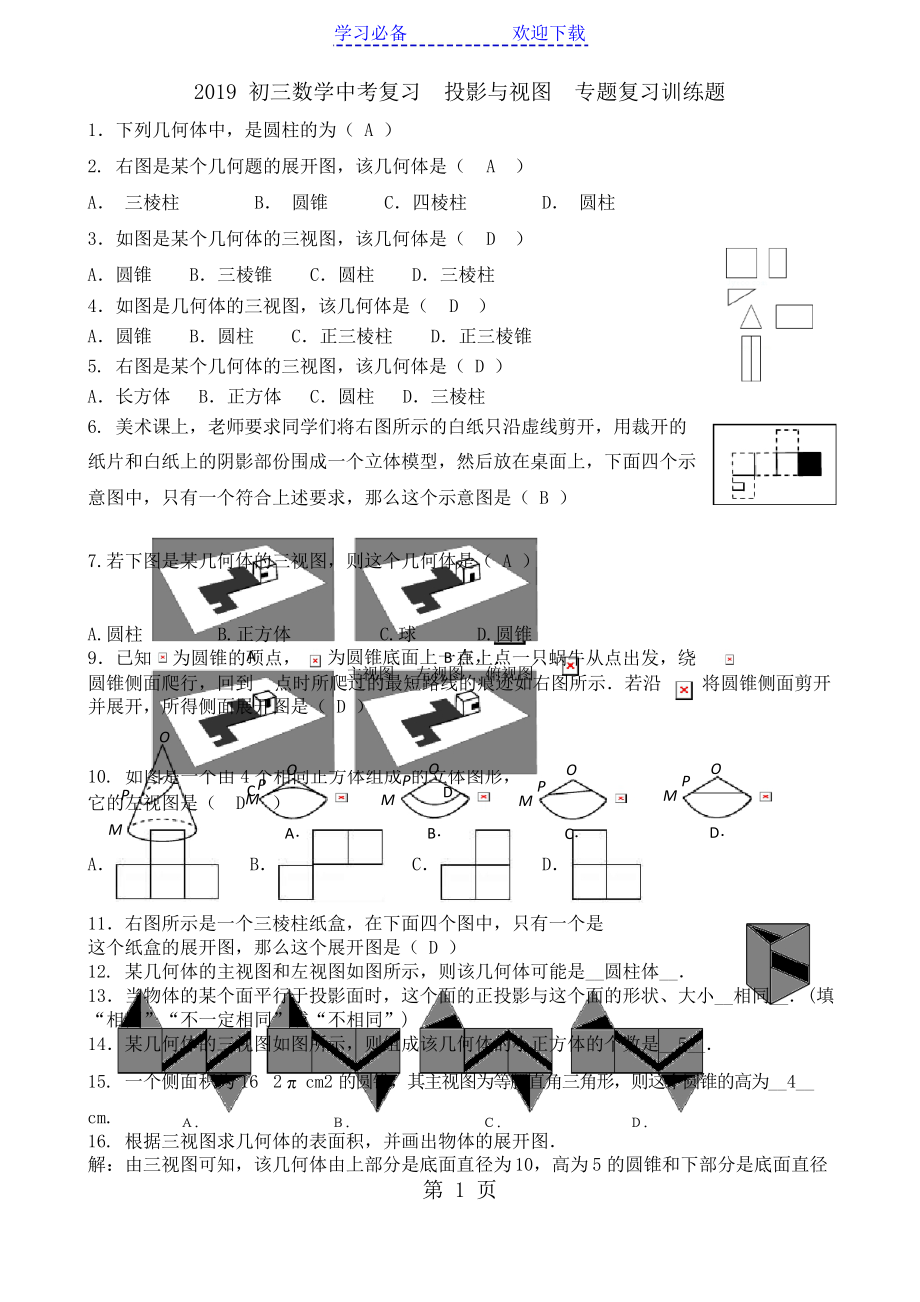
1、圓錐側(cè)面爬行，回到?? 點(diǎn)時(shí)所爬過(guò)的最短路線的痕跡如右圖所示．若沿???? 將圓錐側(cè)面剪開(kāi) 學(xué)習(xí)必備 歡迎下載 2019?初三數(shù)學(xué)中考復(fù)習(xí) 投影與視圖 專(zhuān)題復(fù)習(xí)訓(xùn)練題 1．下列幾何體中，是圓柱的為（?A?） 2.?右圖是某個(gè)幾何題的展開(kāi)圖，該幾何體是（ A ） A．?三棱柱 B．?圓錐 C．四棱柱 D．?圓柱 3．如圖是某個(gè)幾何體的三視圖，該幾何體是（ D ） A．圓錐 B．三棱錐 C．圓柱 D．三棱柱 4．如圖是幾何體的三視圖，該幾何體是（ D ） A．圓錐 B．圓柱 C．正三棱柱 D．正三棱錐 5.?右圖是某個(gè)幾何體的三視圖，

2、該幾何體是（?D?） A．長(zhǎng)方體 B．正方體 C．圓柱 D．三棱柱 6.?美術(shù)課上，老師要求同學(xué)們將右圖所示的白紙只沿虛線剪開(kāi)，用裁開(kāi)的 紙片和白紙上的陰影部份圍成一個(gè)立體模型，然后放在桌面上，下面四個(gè)示 意圖中，只有一個(gè)符合上述要求，那么這個(gè)示意圖是（?B?） 7.若下圖是某幾何體的三視圖，則這個(gè)幾何體是（?A?） A.圓柱 B.正方體 C.球 D.圓錐 A 為圓錐底面上一點(diǎn)，點(diǎn) 9．已知 為圓錐的頂點(diǎn)， B在上．一只蝸牛從點(diǎn)出發(fā)，繞 主視圖 左視圖 俯視圖 并展開(kāi)，所得側(cè)面展開(kāi)圖是（?D?） O 10.

3、??如圖是一個(gè)由?4?個(gè)相同正方體組成P的立體圖形， C?P D P 它的左視圖是（?? DM??） O O O P M M  M?P O M A． B． C． D． A． B． C． D． 11．右圖所示是一個(gè)三棱柱紙盒，在下面四個(gè)圖中，只有一個(gè)是 這個(gè)紙盒的展開(kāi)圖，那么這個(gè)展開(kāi)圖是（?D?） 12.?某幾何體的主視圖和左視圖如圖所示，則該幾何體可能是__圓柱體__． 13．當(dāng)物體的某個(gè)面平行于投影面時(shí)，這個(gè)面的正投影與這個(gè)面的形狀、大小__相同__．(填 “相同”“不一定相同”或“不相同”) 14．某幾何體

4、的三視圖如圖所示，則組成該幾何體的小正方體的個(gè)數(shù)是__5__． 15.?一個(gè)側(cè)面積為?16?2π?cm2?的圓錐，其主視圖為等腰直角三角形，則這個(gè)圓錐的高為_(kāi)_4__ cm. Ａ．?????????????????Ｂ．?????????????????Ｃ．?????????????????Ｄ． 16.?根據(jù)三視圖求幾何體的表面積，并畫(huà)出物體的展開(kāi)圖． 解：由三視圖可知，該幾何體由上部分是底面直徑為?10，高為?5?的圓錐和下部分是底面直徑 第?1?頁(yè) 得圓錐母線長(zhǎng)?R＝5???2，S?圓錐表面積＝??lR＝??×10π?×5???2＝25???2π?，∴

5、S?表面積＝π?×52 DG＝CA＝30??m．∵EF∥AB，∴?FH BG?? DG???????????????????????????????????????????? BG 學(xué)習(xí)必備 歡迎下載 為?10，高為?20?的圓柱組成，物體的展開(kāi)圖如圖．圓錐、圓柱底面半徑為?r＝5，由勾股定理 1 1 2 2 ＋10π?×20＋25?2π?＝225π?＋25?2π?＝(225＋25?2)π 17.?小明想利用太陽(yáng)光測(cè)量樓高，他帶著皮尺來(lái)到一棟樓下，發(fā)現(xiàn)對(duì)面墻上有這棟樓的影子， 針對(duì)這種情況，他設(shè)計(jì)了一種測(cè)量方案，具體測(cè)量情況如下： 如圖，小明邊移動(dòng)邊

6、觀察，發(fā)現(xiàn)站到點(diǎn)?E?處時(shí)，可以使自己落在墻上的影子與這棟樓落 在墻上的影子重疊，且高度恰好相同．此時(shí)，測(cè)得小明落在墻上的影子高度?CD＝1.2?m，CE ＝0.8?m，CA＝30?m(點(diǎn)?A，E，C?在同一直線上)．已知小明的身高?EF?是?1.7?m，請(qǐng)你幫小明 求出樓高?AB.(結(jié)果精確到?0.1?m) 解：過(guò)點(diǎn)?D?作?DG⊥AB，分別交?AB，EF?于點(diǎn)?G，H，則?EH＝AG＝CD＝1.2?m，DH＝CE＝0.8?m， DH 0.5 ＝ .由題意，知?FH＝EF－EH＝1.7－1.2＝0.5(m)，∴ ＝ 0.8 30  ，解得?BG＝18.75(m)，∴AB＝BG＋AG＝18.75＋1.2＝19.95(m)≈20.0(m)，∴樓高?AB?約 為?20.0?m 第?2?頁(yè)