《四川省開江縣高中數(shù)學(xué) 第一章 集合與函數(shù)的概念 1.3.1 函數(shù)的單調(diào)性（1）課件 新人教A版必修1》由會員分享，可在線閱讀，更多相關(guān)《四川省開江縣高中數(shù)學(xué) 第一章 集合與函數(shù)的概念 1.3.1 函數(shù)的單調(diào)性（1）課件 新人教A版必修1（22頁珍藏版）》請在裝配圖網(wǎng)上搜索。

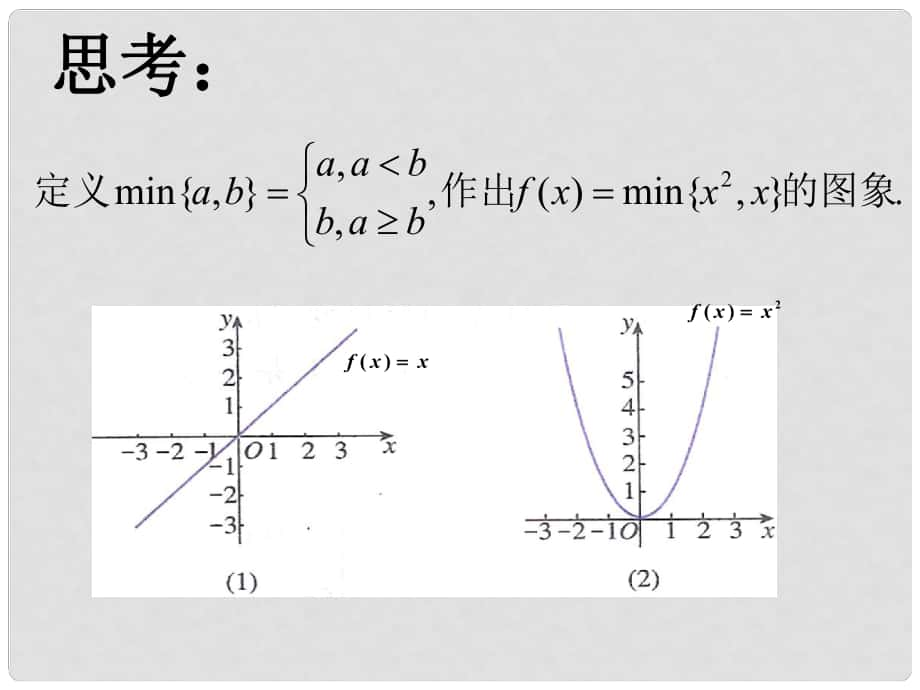
1、.,min)(,min2的圖象作出定義xxxfbabbaaba思考：思考：()fxx 2()fxx 函數(shù)是描述事物運動變化規(guī)律的數(shù)學(xué)模型函數(shù)是描述事物運動變化規(guī)律的數(shù)學(xué)模型.如果如果了解了函數(shù)的變化規(guī)律，那么也就基本把握了相應(yīng)了解了函數(shù)的變化規(guī)律，那么也就基本把握了相應(yīng)事物的變化規(guī)律事物的變化規(guī)律. 觀察下列兩個函數(shù)的圖象，你能說說它們分別反觀察下列兩個函數(shù)的圖象，你能說說它們分別反映了相應(yīng)函數(shù)的哪些變化規(guī)律？映了相應(yīng)函數(shù)的哪些變化規(guī)律？ ()fxx 2()fxx ( )f xx 2( )f xx 函數(shù)函數(shù) f(x)=x 的圖象的圖象由左至右是由左至右是上升上升的；的；函數(shù)函數(shù) f(x)=x2

2、的圖象的圖象在在y軸左側(cè)是軸左側(cè)是下降下降的的,在在y軸右側(cè)是軸右側(cè)是上升上升的的.1.3.1 函數(shù)的單調(diào)性（函數(shù)的單調(diào)性（1）xOy由由左左至至右右軸軸左左側(cè)側(cè)y圖圖象象下下降降由由左左至至右右軸軸右右側(cè)側(cè)y圖圖象象上上升升9410149f(x)3210-1-2-3x的的增增大大隨隨著著 x0 ,(區(qū)間區(qū)間減小減小對應(yīng)對應(yīng))(xf的的增增大大隨隨著著x), 0 區(qū)間區(qū)間增大增大對應(yīng)對應(yīng))(xf函函數(shù)數(shù)的的單單調(diào)調(diào)性性呢呢？如如何何準準確確而而簡簡潔潔地地刻刻畫畫 函數(shù)圖象的函數(shù)圖象的“上升上升” “下降下降”反映了函數(shù)的反映了函數(shù)的一個基本性質(zhì)一個基本性質(zhì) 如何描述函數(shù)圖象的如何描述函數(shù)圖象

3、的“上升上升” “下降下降”呢呢？ 單調(diào)性單調(diào)性2( )f xx x01234f(x) 014916f(x)x1x)(1xf2x)(2xf10 10 31 91 42 164 21xx 12()()f xf x至至少少需需要要兩兩組組數(shù)數(shù)來來刻刻畫畫任意任意.)(),()(,:)(212121上是增函數(shù)上是增函數(shù)在區(qū)間在區(qū)間函數(shù)函數(shù)那么就說那么就說時，都有時，都有當當?shù)闹档闹瞪系娜我鈨蓚€自變量上的任意兩個自變量內(nèi)某個區(qū)間內(nèi)某個區(qū)間如果對于定義域如果對于定義域的定義域為的定義域為一般地，設(shè)函數(shù)一般地，設(shè)函數(shù)DxfxfxfxxxxDIIxf xOy2( )f xx .)(),()(,:)(2121

4、21上上是是增增函函數(shù)數(shù)在在區(qū)區(qū)間間函函數(shù)數(shù)那那么么就就說說時時，都都有有當當?shù)牡闹抵瞪仙系牡娜稳我庖鈨蓛蓚€個自自變變量量內(nèi)內(nèi)某某個個區(qū)區(qū)間間如如果果對對于于定定義義域域的的定定義義域域為為一一般般地地，設(shè)設(shè)函函數(shù)數(shù)DxfxfxfxxxxDIIxf 增函數(shù)的定義：增函數(shù)的定義：.)(),()(,:)(212121上上是是減減函函數(shù)數(shù)在在區(qū)區(qū)間間函函數(shù)數(shù)那那么么就就說說時時，都都有有當當?shù)牡闹抵瞪仙系牡娜稳我庖鈨蓛蓚€個自自變變量量內(nèi)內(nèi)某某個個區(qū)區(qū)間間如如果果對對于于定定義義域域的的定定義義域域為為一一般般地地，設(shè)設(shè)函函數(shù)數(shù)DxfxfxfxxxxDIIxf 減函數(shù)的定義：減函數(shù)的定義：).()()

5、,()()()(,:)(21212121減減函函數(shù)數(shù)上上是是增增函函數(shù)數(shù)在在區(qū)區(qū)間間那那么么就就說說函函數(shù)數(shù)時時，都都有有，當當值值上上的的任任意意兩兩個個自自變變量量的的內(nèi)內(nèi)某某個個區(qū)區(qū)間間如如果果對對于于定定義義域域的的定定義義域域為為一一般般地地，設(shè)設(shè)函函數(shù)數(shù)DxfxfxfxfxfxxxxDIIxf 定定 義：義： 如果如果y=f(x)在某個區(qū)間是增函數(shù)或減函數(shù)在某個區(qū)間是增函數(shù)或減函數(shù),那么那么就說函數(shù)就說函數(shù)y=f(x)在這一區(qū)間具有（嚴格的）在這一區(qū)間具有（嚴格的）單調(diào)性單調(diào)性，這一區(qū)間叫做這一區(qū)間叫做y=f(x)的的單調(diào)區(qū)間單調(diào)區(qū)間.xOy)., 00 ,()(2 單增區(qū)間是單增

6、區(qū)間是；的單減區(qū)間是的單減區(qū)間是函數(shù)函數(shù)xxf函數(shù)單調(diào)性的定義：函數(shù)單調(diào)性的定義：.),(1)(上是增函數(shù)上是增函數(shù)在區(qū)間在區(qū)間函數(shù)函數(shù) xxfxOyxOy.), 0(),0 ,(1)(上是減函數(shù)上是減函數(shù)在區(qū)間在區(qū)間函數(shù)函數(shù) xxf能寫成并集么？能寫成并集么？例例1 1. .定義在閉區(qū)間定義在閉區(qū)間-5，5上的函數(shù)上的函數(shù)y=f(x)的圖象，的圖象，根據(jù)圖象說出根據(jù)圖象說出y=f(x)的單調(diào)區(qū)間，以及在每一單調(diào)的單調(diào)區(qū)間，以及在每一單調(diào)區(qū)間上，區(qū)間上，y=f(x)是增函數(shù)還是減函數(shù)是增函數(shù)還是減函數(shù). .解：解：函數(shù)的單調(diào)區(qū)間有函數(shù)的單調(diào)區(qū)間有-5,-2),-2,1),1,3),3,5; 其

7、中其中y=f(x)在區(qū)間在區(qū)間-5,-2)，1,3)上是減函數(shù)，上是減函數(shù)， 在區(qū)間在區(qū)間-2,1)，3,5上是增函數(shù)上是增函數(shù). .練習(xí)練習(xí)1練習(xí)練習(xí)1練習(xí)練習(xí)1 1（3 3）、求函數(shù)）、求函數(shù)y=|=|x2 2-2-2x-3|-3|的單調(diào)區(qū)間。的單調(diào)區(qū)間。例例2 2、利用定義證明：函數(shù)、利用定義證明：函數(shù)f( (x)=)=x+ + 在在(0,1)(0,1)上為上為減函數(shù)。減函數(shù)。x1證明函數(shù)單調(diào)性的方法步驟證明函數(shù)單調(diào)性的方法步驟 1. 任取任取x1，x2D，且，且x1x2；2. 作差作差f(x1)f(x2)；3. 變形（通常是因式分解和配方）；變形（通常是因式分解和配方）；4. 定號（即

8、判斷差定號（即判斷差f(x1)f(x2)的正負）；的正負）；5.下結(jié)論（即指出函數(shù)下結(jié)論（即指出函數(shù)f(x)在給定的區(qū)間在給定的區(qū)間D上的上的單調(diào)性）單調(diào)性） 利用定義證明函數(shù)利用定義證明函數(shù)f(x)在給定的區(qū)間在給定的區(qū)間D上的單上的單調(diào)性的一般步驟：調(diào)性的一般步驟：17練習(xí)練習(xí)2 2、利用定義證明：函數(shù)、利用定義證明：函數(shù)f( (x)=)=x+ + 在在(1, )(1, )上為增函數(shù)。上為增函數(shù)。x1 若若 呢？呢？ 0)()(2121xxxfxf思考思考1 1：對于函數(shù)對于函數(shù)f( (x) )定義域內(nèi)某個區(qū)間定義域內(nèi)某個區(qū)間D D上的任意上的任意兩個自變量的值兩個自變量的值x1 1, ,

9、x2 2，若，若 ，則函數(shù)，則函數(shù)f( (x) )在區(qū)間在區(qū)間D D上的單調(diào)性如何？上的單調(diào)性如何？0)()(2121xxxfxf19思考思考2 2：若若f( (x) )在區(qū)間在區(qū)間D D上為增函數(shù)，且上為增函數(shù)，且a為非零常為非零常數(shù)，則函數(shù)數(shù)，則函數(shù)a+ +f( (x) )、af( (x) )的單調(diào)性如何？的單調(diào)性如何？思考思考3 3：若函數(shù)若函數(shù)f( (x) )、g( (x) )在區(qū)間在區(qū)間D D上都是增函數(shù)，上都是增函數(shù)，則函數(shù)則函數(shù)f( (x)+)+g( (x) )、f( (x)-)-g( (x) )在區(qū)間在區(qū)間D D上的單調(diào)性上的單調(diào)性能否確定？能否確定？20思考思考4 4：若函數(shù)若函數(shù)f( (x) )在區(qū)間在區(qū)間D D上是增函數(shù)，則函數(shù)上是增函數(shù)，則函數(shù) 在區(qū)間在區(qū)間D D上是增函數(shù)嗎？函數(shù)上是增函數(shù)嗎？函數(shù) 在在區(qū)間區(qū)間D D上是減函數(shù)嗎？上是減函數(shù)嗎？)(xfy )(1xfy 21思考思考5:5:下列圖象表示的函數(shù)是增函數(shù)嗎？下列圖象表示的函數(shù)是增函數(shù)嗎？ xy0 0圖圖1 1xy0 0圖圖2 一般地，若函數(shù)一般地，若函數(shù)f( (x) )在區(qū)間在區(qū)間A A、B B上是單調(diào)函數(shù)，上是單調(diào)函數(shù)，那么那么f( (x) )在區(qū)間在區(qū)間ABAB上一定是單調(diào)函數(shù)嗎？上一定是單調(diào)函數(shù)嗎？22