《2018年秋九年級數(shù)學下冊 第3章 三視圖與表面展開圖 3.4 簡單幾何體的表面展開圖（3）練習 （新版）浙教版》由會員分享，可在線閱讀，更多相關《2018年秋九年級數(shù)學下冊 第3章 三視圖與表面展開圖 3.4 簡單幾何體的表面展開圖（3）練習 （新版）浙教版（4頁珍藏版）》請在裝配圖網上搜索。

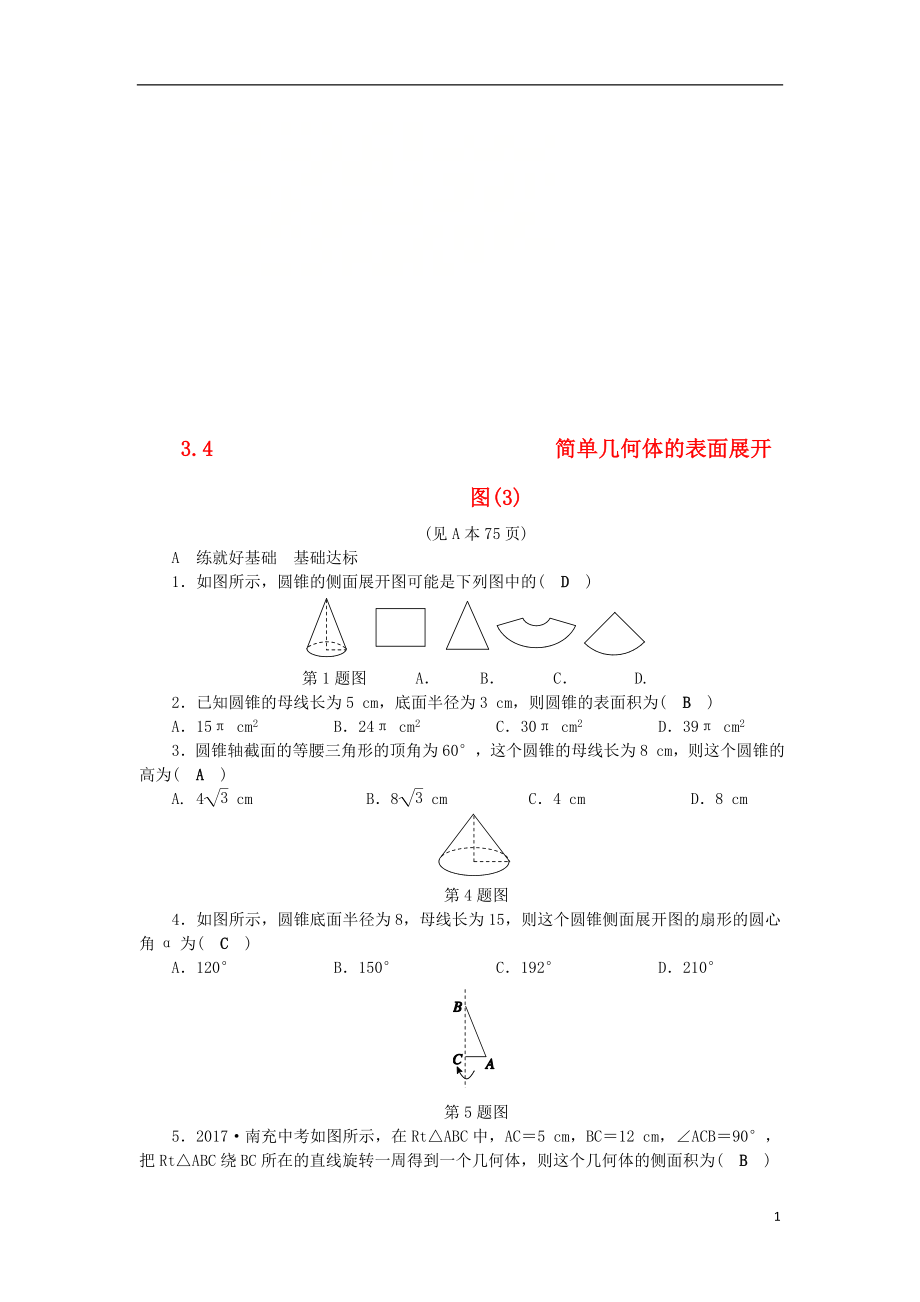
1、 3.4 簡單幾何體的表面展開圖(3) (見A本75頁) A　練就好基礎　基礎達標 1．如圖所示，圓錐的側面展開圖可能是下列圖中的(　D　) 第1題圖　　　A．　 　B．　　　C．　 　　D. 2．已知圓錐的母線長為5 cm，底面半徑為3 cm，則圓錐的表面積為(　B　) A．15π cm2 B．24π cm2 C．30π cm2 D．39π cm2 3．圓錐軸截面的等腰三角形的頂角為60°，這個圓錐的母線長為8 cm，則這個圓錐的高為(　A　) A. 4 cm B．8 cm C．4 cm D．8 cm 第4題圖 4．如圖所示，

2、圓錐底面半徑為8，母線長為15，則這個圓錐側面展開圖的扇形的圓心角α為(　C　) A．120° B．150° C．192° D．210° 第5題圖 5．2017·南充中考如圖所示，在Rt△ABC中，AC＝5 cm，BC＝12 cm，∠ACB＝90°，把Rt△ABC繞BC所在的直線旋轉一周得到一個幾何體，則這個幾何體的側面積為(　B　) A．60π cm2 B．65π cm2 C．120π cm2 D．130π cm2 6．若一個圓錐的側面展開圖是半徑為18 cm，圓心角為240°的扇形，則這個圓錐的底面半徑長是(　C　) A．6 cm

3、 B．9 cm C．12 cm D．18 cm 7．已知圓錐的底面半徑為5 cm，側面積為60π cm2，則這個圓錐的母線長為__12__ cm，它的側面展開圖的圓心角是__150°__． 8．圓錐的側面積為18π cm2，其側面展開圖是半圓，則圓錐的底面半徑是__3__ cm. 第9題圖 9．如圖所示的扇形是一個圓錐的側面展開圖，若∠AOB＝120°，的長為12π cm，則該圓錐的側面積為__108_π__cm2. 10．如圖所示，現(xiàn)有一圓心角為90°.半徑為80 cm的扇形鐵片，用它恰好圍成一個圓錐形的量筒，用其他鐵片再做一個圓形蓋子把量筒底面密封(接縫都忽略

4、不計)． 求：(1)該圓錐蓋子的半徑為多少cm? (2)制作這個密封量筒，共用鐵片多少cm2？(結果保留π) 第10題圖 解：(1)圓錐的底面周長＝＝40π(cm)， 設圓錐底面圓的半徑為r，則2πr＝40π， 解得r＝20， 即該圓錐蓋子的半徑為20 cm. (2)由題意得：S＝S側＋S底＝π×802＋400π＝2000π (cm2)， 即共用鐵片2000π cm2. B　更上一層樓　能力提升 11．2017·綿陽中考“趕陀螺”是一項深受人們喜愛的運動，如圖所示是一個陀螺的立體結構圖．已知底面圓的直徑AB＝8 cm，圓柱體部分的高BC＝6 cm，圓錐體部分的高C

5、D＝3 cm，則這個陀螺的表面積是(　C　) 第11題圖 A．68π cm2 B．74π cm2 C．84π cm2 D．100π cm2 第12題圖 12．如圖所示，從直徑為2 m的圓形鐵皮上剪出一個圓心角是90°的扇形ABC(A，B，C三點在⊙O上)，將剪下來的扇形圍成一個圓錐的側面，則該圓錐的底面圓的半徑是____ m. 第13題圖 13．如圖所示，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，若把Rt△ABC繞邊AB所在直線旋轉一周，所得幾何體的全面積為__8π__(結果保留π). 第14題圖 14．如圖所示，扇形O

6、BC是圓錐的側面展開圖，圓錐的母線OB＝l，底面圓的半徑HB＝r. (1)當l＝2r時，求∠BOC的度數(shù)； (2)當l＝3r，l＝4r時，分別求∠BOC的度數(shù)；(直接寫出結果) (3)當l＝nr(n為大于1的整數(shù))時，猜想∠BOC的度數(shù)．(直接寫出結果) 解：(1)設∠BOC＝n，則得n＝180°， ∴∠BOC的度數(shù)為180°. (2)當l＝3r時，∠BOC＝120°；當l＝4r時，∠BOC＝90°. (3)∠BOC＝° C　開拓新思路　拓展創(chuàng)新 15．2017·岱岳二模如圖是某幾何體的三視圖及相關數(shù)據，則該幾何體的全面積是(　B　) 第15題圖 A．15π

7、B．24π C．20π D．10π 16．在一次科學探究實驗中，小明將半徑為5 cm的圓形濾紙片按圖1所示的步驟進行折疊，并圍成圓錐形． (1) 取一漏斗(如圖2所示)，上部的圓錐形內壁(忽略漏斗管口處)的母線OB長為6 cm，開口圓的直徑為6 cm.當濾紙片重疊部分為三層，且每層為圓時，濾紙圍成的圓錐形放入該漏斗中，能否緊貼此漏斗的內壁(忽略漏斗管口處)？請你用所學的數(shù)學知識說明． (2)假設有一特殊規(guī)格的漏斗，其母線長為6 cm，開口圓的直徑為7.2 cm，現(xiàn)將同樣大小的濾紙圍成重疊部分為三層的圓錐形，放入此漏斗中，且能緊貼漏斗內壁．問重疊部分每層的面積為多少？

8、圖1 圖2 第16題圖 解：(1)∵表面緊貼的兩圓錐形的側面展開圖為圓心角相同的兩扇形，∴表面是否緊貼只需考慮展開圖的圓心角是否相等，由于濾紙圍成的圓錐形只有最外層側面緊貼漏斗內壁，故只考慮該濾紙圓錐最外層的側面和漏斗內壁圓錐側面的關系．將圓形濾紙片按圖示的步驟折成四層且每層為圓，則圍成的圓錐形的側面積＝S濾紙圓＝S濾紙圓，∴它的側面展開圖是半圓，其圓心角為180°，如將漏斗內壁構成的圓錐側面也抽象地展開，展開的扇形弧長為πd＝π×6＝6π(cm)，該側面展開圖的圓心角為6π÷6×＝180°. 由此可以看出兩圓錐的側面展開得到的扇形，它們的圓心角相等，∴該濾紙圍成的圓錐形必能緊貼漏斗內壁． (2)如果抽象地將母線長為6 cm，開口圓直徑為7.2 cm的特殊規(guī)格的漏斗內壁圓錐側面展開，得到的扇形弧長為7.2π cm，圓心角為7.2π÷6×＝216°，濾紙片如緊貼漏斗壁，其圍成圓錐的最外層側面展開圖的圓心角也應為216°. 又∵重疊部分每層面積為圓形濾紙片的面積減去圍成圓錐的最外層側面展開圖的面積的差的一半，∴濾紙重疊部分每層面積＝÷2＝5π(cm2)． 4