4、圖K26-7
9.[2016·齊齊哈爾]如圖K26-7��,若以平行四邊形一邊AB為直徑的圓恰好與對(duì)邊CD相切于點(diǎn)D�����,則∠C=________度.
10.[2017·鎮(zhèn)江]如圖K26-8,AB是⊙O的直徑�����,AC與⊙O相切����,CO交⊙O于點(diǎn)D.若∠CAD=30°,則∠BOD=________.
圖K26-8
圖K26-9
11.[2016·德州]《九章算術(shù)》是我國(guó)古代內(nèi)容極為豐富的數(shù)學(xué)名著.書中有下列問題“今有勾八步�,股十五步,問勾中容圓徑幾何�?”其意思是今有直角三角形,勾(短直角邊)長(zhǎng)為8步���,股(長(zhǎng)直角邊)長(zhǎng)為15步��,如圖K26-9所示����,問該直角三角形能容納的圓形(內(nèi)
5���、切圓)直徑是多少�?________.
圖K26-10
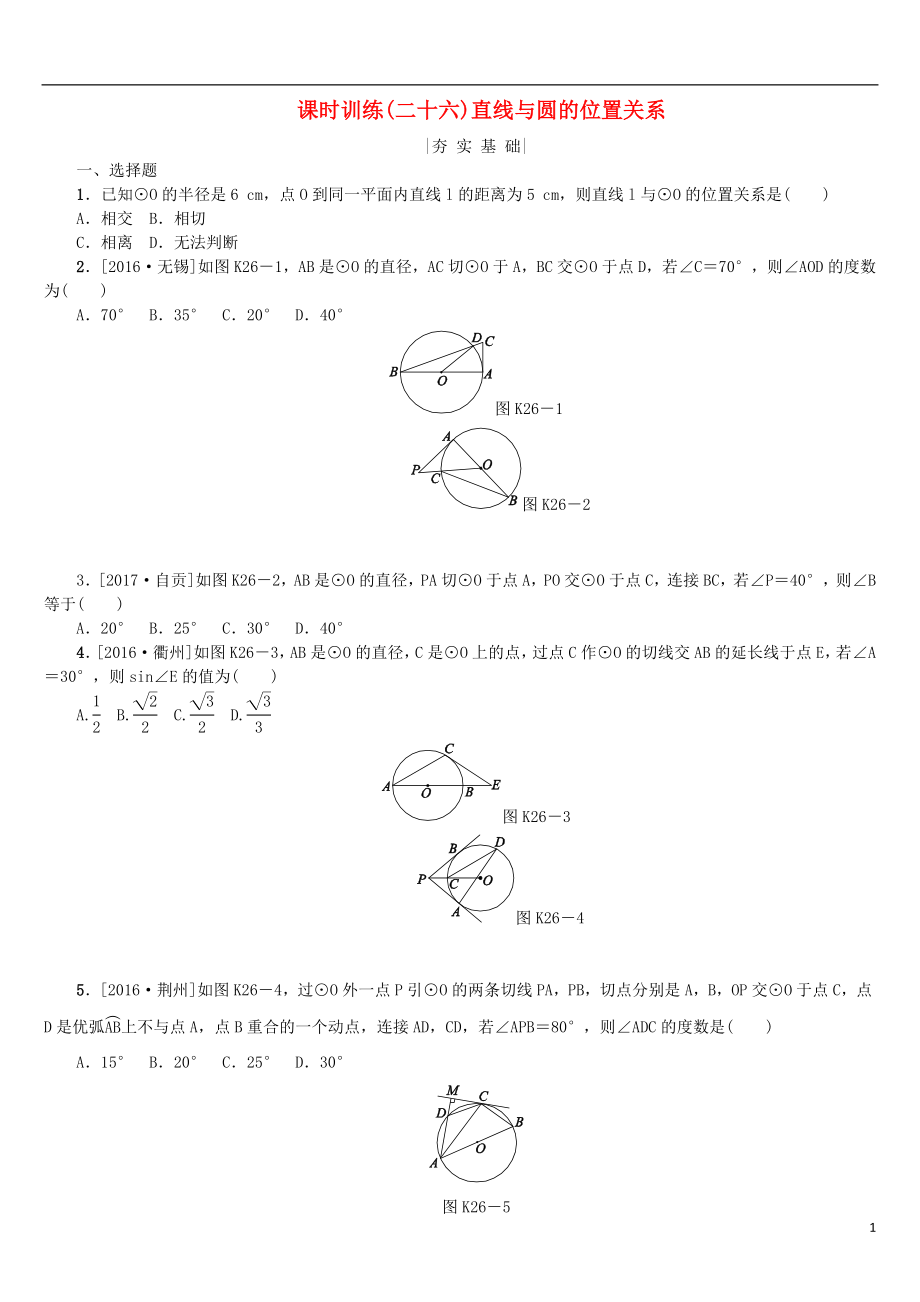
12.[2017·湖州]如圖K26-10,已知∠AOB=30°�����,在射線OA上取點(diǎn)O1���,以O(shè)1為圓心的圓與OB相切�;在射線O1A上取點(diǎn)O2���,以O(shè)2為圓心�,O2O1為半徑的圓與OB相切���;在射線O2A上取點(diǎn)O3�,以O(shè)3為圓心���,O3O2為半徑的圓與OB相切;…���;在射線O9A上取點(diǎn)O10����,以O(shè)10為圓心,O10O9為半徑的圓與OB相切.若⊙O1的半徑為1��,則⊙O10的半徑長(zhǎng)是________.
三�、解答題
13.[2017·濟(jì)寧]如圖K26-11,已知⊙O的直徑AB=12����,弦AC=10,D是的中點(diǎn)�����,過點(diǎn)D作DE⊥AC交AC的延長(zhǎng)線于點(diǎn)E.
6�����、
(1)求證:DE是⊙O的切線���;
(2)求AE的長(zhǎng).
圖K26-11
14.[2017·遵義]如圖K26-12�,PA�����,PB是⊙O的切線�,A�,B為切點(diǎn)��,∠APB=60°��,連接PO并延長(zhǎng)與⊙O交于C點(diǎn)�,連接AC,BC.
(1)求證:四邊形ACBP是菱形����;
(2)若⊙O半徑為1,求菱形ACBP的面積.
圖K26-12
15.[2016·漳州]如圖K26-13�����,AB為⊙O的直徑���,點(diǎn)E在⊙O上����,C為的中點(diǎn)���,過點(diǎn)C作直線CD⊥AE于D,連接AC�,BC.
(1)試判斷直線CD與⊙O的位置關(guān)系����,并說明理由�;
(2)若AD=2,AC=����,求AB的長(zhǎng).
圖K26-13
7、
|拓 展 提 升|
16.[2016·衡陽]如圖K26-14�,在平面直角坐標(biāo)系中,△ABC的三個(gè)頂點(diǎn)坐標(biāo)分別為A(-�,0),B(����,0),C(0����,3).
(1)求△ABC的內(nèi)切圓⊙D的半徑;
(2)過點(diǎn)E(0�����,-1)的直線與⊙D相切于點(diǎn)F(點(diǎn)F在第一象限)�����,求直線EF的表達(dá)式;
(3)以(2)為條件���,P為直線EF上一點(diǎn)����,以P為圓心���,以2 為半徑作⊙P����,若⊙P上存在一點(diǎn)到△ABC三個(gè)頂點(diǎn)的距離相等�����,求此時(shí)圓心P的坐標(biāo).
圖K26-14
參考答案
1.A [解析]
8����、設(shè)⊙O的半徑為r,點(diǎn)O到直線l的距離為d.
∵d=5 cm����,r=6 cm�����,∴d<r,
∴直線l與圓相交.故選A.
2.D [解析] 依題意��,AC切⊙O于點(diǎn)A���,且AB是圓O的直徑��,∴AB⊥AC���,∴∠CAB=90°.
又∵∠C=70°,∴∠CBA=20°.∴∠DOA=40°.
3.B [解析] ∵PA切⊙O于點(diǎn)A�����,∴∠PAO=90°.∵∠P=40°��,∴∠POA=180°-90°-40°=50°.∵OC=OB�����,∴∠B=∠OCB.∵∠POA是△COB的外角�����,∴∠B+∠OCB=50°,∴∠B=50°÷2=25°.
4.A [解析] 連接OC�,根據(jù)直線CE與⊙O相切可得OC⊥CE.又∠A=30
9、°�,∴∠BOC=2∠A=60°,
∴∠E=90°-∠BOC=30°�����,∴sin∠E=sin30°=.
5.C [解析] 連接OB��,OA���,易得∠BOA=360°-90°-90°-80°=100°.又∵=�����,∴∠AOC=∠BOC=50°�����,∴∠ADC=∠AOC=25°.
6.A [解析] 連接OC�,因?yàn)镃M為⊙O的切線,所以O(shè)C⊥MC.因?yàn)锳M⊥MC����,所以AM∥OC.所以∠MAB=∠COB,∠MAC=∠OCA.因?yàn)镺B=OC�,所以∠OCB=∠OBC=55°,所以∠MAB=∠COB=180°-2×55°=70°��,因?yàn)镺A=OC�,所以∠OAC=∠OCA=∠MAC�,所以∠MAC=∠MAB=35°
10、.因?yàn)椤螦DC+∠ABC=180°��,所以∠ADC=180°-∠ABC=180°-55°=125°.所以∠ACD=180°-∠ADC-∠MAC=180°-125°-35°=20°.
7.D [解析] 如圖�����,y=-x平分第二���、四象限����,將y=-x向上平移為y=-x+b(b>0)���,當(dāng)y=-x+b與圓相切時(shí)����,b最大,由平移知∠CAO=∠AOC=45°��,OC=2�����,∴OA=b=2 �,同理將y=-x向下平移為y=-x+b(b<0)��,當(dāng)y=-x+b與圓相切時(shí)�����,b最小,同理可得b=-2 ����,∴當(dāng)y=-x+b與圓相交時(shí),-2 <b<2 .
8.4 [解析] ∵PA切⊙O于點(diǎn)A��,
∴OA⊥PA.在Rt△OPA
11���、中�����,OP=5��,OA=3�,
∴PA==4.故答案為4.
9.45 [解析] 連接OD,則OD⊥CD���,∴△AOD是等腰直角三角形,∴∠C=∠A=45°.
10.120° [解析] 由AC與⊙O相切可得∠CAO=90°�����,而∠CAD=30°���,故∠OAD=60°.由OA=OD����,可得∠OAD=∠ODA=60°�����,∠BOD=∠OAD+∠ODA=60°+60°=120°.
11.6步 [解析] 過點(diǎn)O分別作OD⊥AC,OE⊥AB����,OF⊥BC,
設(shè)⊙O的半徑是r�,
∵⊙O是△ABC的內(nèi)切圓,
∴OD=OE=OF=r.
∵AB=15�,BC=8,
在Rt△ABC中��,
由勾股定理得����,AC==17
12、�,
∴×15×8=×(15+17+8)×r,
∴r=3.
12.29 [解析] 作O1C�、O2D、O3E分別垂直O(jiān)B���,∵∠AOB=30°�,∴OO1=2CO1�����,OO2=2DO2,OO3=2EO3�����,∵O1O2=DO2�,O2O3=EO3,
∴圓的半徑呈2倍遞增����,∴⊙On的半徑為2n-1CO1,∵⊙O1的半徑為1����,∴⊙O10的半徑長(zhǎng)=29,故答案為29.
13.解:(1)證明:連接OD��,∵D是的中點(diǎn)�,
∴=.
∴∠BOD=∠BAC��,
∴OD∥AE.
∵DE⊥AC�����,
∴∠AED=90°.
∴∠ODE=90°.
∴OD⊥DE.
∴DE是⊙O的切線.
(2)過點(diǎn)O作OF⊥
13�����、AC于點(diǎn)F,
∵AC=10���,
∴AF=CF=AC=×10=5.
∵∠OFE=∠DEF=∠ODE=90°���,
∴四邊形OFED是矩形,
∴FE=OD=AB.
∵AB=12����,
∴FE=6,
∴AE=AF+FE=5+6=11.
14.解:(1)證明:連接AO�����,BO��,∵PA��、PB是⊙O的切線����,∴∠OAP=∠OBP=90°,PA=PB��,∠APO=∠BPO=∠APB=30°,∴∠AOP=60°�����,∵OA=OC����,∴∠OAC=∠OCA,∵∠AOP=∠CAO+∠ACO�����,∴∠ACO=30°�,∴∠ACO=∠APO,∴AC=AP����,同理BC=PB,∴AC=BC=BP=AP�,∴四邊形ACBP是菱形.
(2
14���、)連接AB交PC于D���,∴AD⊥PC�,∵OA=1���,∠AOP=60°���,∴AD=OA=,∴PD=��,∴PC=3�����,AB=����,∴菱形ACBP的面積=AB·PC=.
15.解:(1)相切,理由如下:連接OC�����,
∵C為的中點(diǎn)�,∴=,
∴∠1=∠2.
∵∠3=2∠1����,∴∠3=∠OAE�,
∴OC∥AD.
∵CD⊥AD�����,
∴OC⊥CD.
∴CD是⊙O的切線.
(2)∵AB為⊙O的直徑�,
∴∠ACB=90°.
∵AD⊥CD,
∴∠ADC=90°�����,
∴∠ACB=∠ADC.
∵∠1=∠2�����,
∴△ABC∽△ACD���,
∴=�����,
∴AB===3.
16.解:(1)連接BD���,
∵B(�����,0
15、)��,C(0����,3),
∴OB=����,OC=3,∴tan∠CBO==����,
∴∠CBO=60°.
∵點(diǎn)D是△ABC的內(nèi)心,∴BD平分∠CBO����,
∴∠DBO=30°,
∴tan∠DBO=��,∴OD=1�,
∴△ABC內(nèi)切圓的半徑為1.
(2)連接DF,過點(diǎn)F作FG⊥y軸于點(diǎn)G.
∵E(0,-1)��,∴OE=1�����,DE=2.
∵直線EF與⊙D相切���,∴∠DFE=90°����,DF=1����,
∴sin∠DEF==,∴∠DEF=30°���,
∴∠GDF=60°.
∴在Rt△DGF中���,∠DFG=30°,∴DG=�,
由勾股定理可求得GF=,∴F(��,).
設(shè)直線EF的表達(dá)式為y=kx+b,
∴解得
∴直線E
16����、F的表達(dá)式為y=x-1.
(3)∵⊙P上存在一點(diǎn)到△ABC三個(gè)頂點(diǎn)的距離相等�����,
∴該點(diǎn)必為△ABC外接圓的圓心.
由(1)可知���,△ABC是等邊三角形����,
∴△ABC外接圓的圓心為點(diǎn)D����,
∴DP=2 .
設(shè)直線EF與x軸交于點(diǎn)H,
令y=0���,代入y=x-1���,
則x=,
∴H(����,0)����,∴FH=.
當(dāng)P在x軸上方時(shí)���,
過點(diǎn)P作PM⊥x軸于M����,
由勾股定理可求得PF=3 ����,
∴PH=PF+FH=.
∵∠DEF=∠HPM=30°,
∴HM=PH=��,PM=5���,
∴OM=2 ����,∴P(2 ��,5).
當(dāng)P在x軸下方時(shí)����,
過點(diǎn)P作PN⊥x軸于點(diǎn)N���,
由勾股定理可求得PF=3 ,
∴PH=PF-FH=.
又∠DEF=30°���,∴∠OHE=60°,
∴sin∠OHE=���,
∴PN=4.
令y=-4��,代入y=x-1�,
∴x=-�����,
∴P(-��,-4).
綜上所述����,若⊙P上存在一點(diǎn)到△ABC三個(gè)頂點(diǎn)的距離相等,則圓心P的坐標(biāo)為(2 ��,5)或(-,-4).
8
 2018年中考數(shù)學(xué)復(fù)習(xí) 第6單元 圓 第26課時(shí) 直線與圓的位置關(guān)系檢測(cè) 湘教版
2018年中考數(shù)學(xué)復(fù)習(xí) 第6單元 圓 第26課時(shí) 直線與圓的位置關(guān)系檢測(cè) 湘教版