《2018年中考數(shù)學(xué)復(fù)習(xí) 第3單元 函數(shù)及其圖象 第11課時(shí) 一次函數(shù)的圖象與性質(zhì)檢測(cè) 湘教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018年中考數(shù)學(xué)復(fù)習(xí) 第3單元 函數(shù)及其圖象 第11課時(shí) 一次函數(shù)的圖象與性質(zhì)檢測(cè) 湘教版（5頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

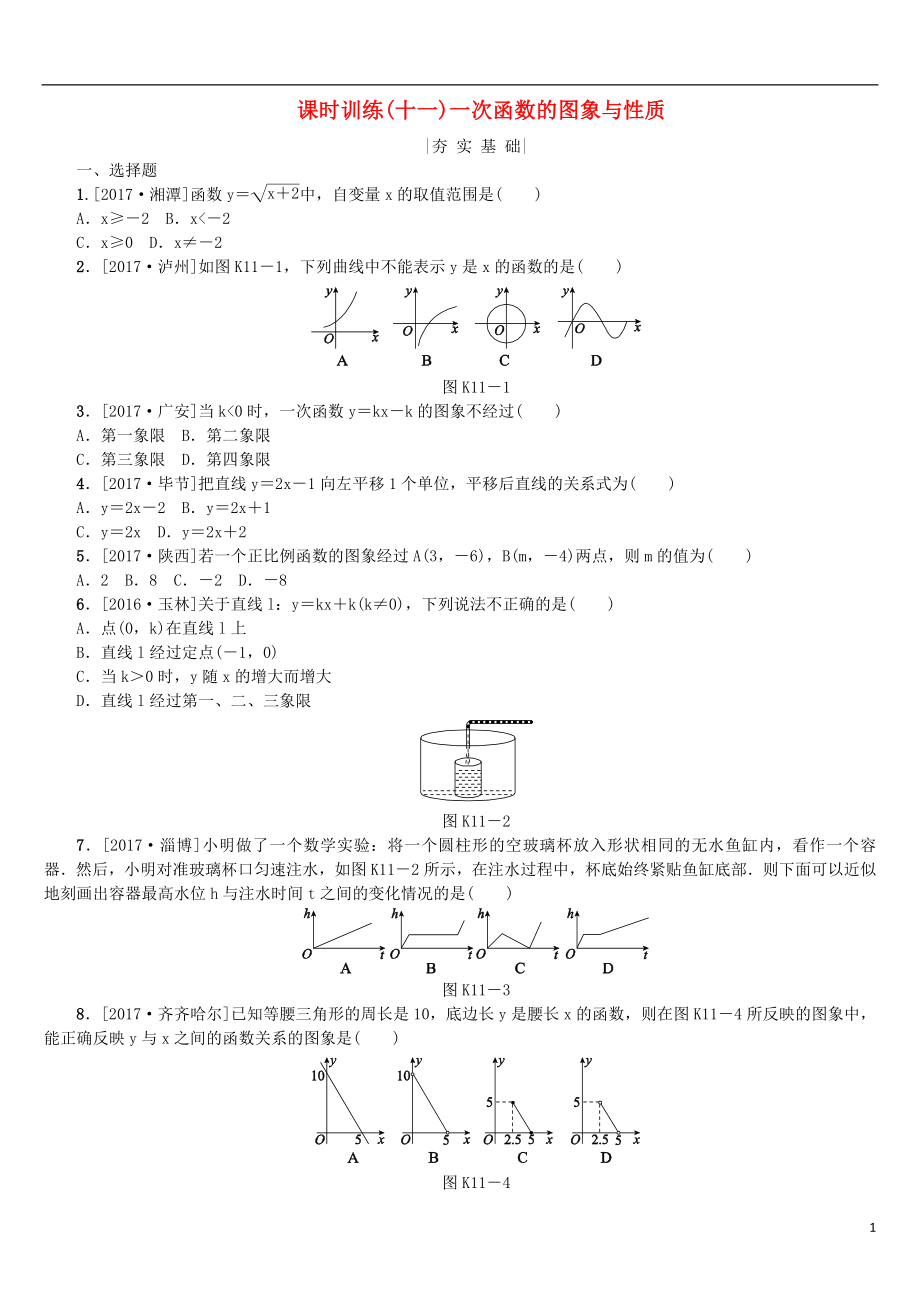
1、 課時(shí)訓(xùn)練(十一)一次函數(shù)的圖象與性質(zhì) |夯 實(shí) 基 礎(chǔ)| 一、選擇題 1.[2017·湘潭]函數(shù)y＝中，自變量x的取值范圍是(　　) A．x≥－2 B．x<－2 C．x≥0 D．x≠－2 2．[2017·瀘州]如圖K11－1，下列曲線中不能表示y是x的函數(shù)的是(　　) 圖K11－1 3．[2017·廣安]當(dāng)k<0時(shí)，一次函數(shù)y＝kx－k的圖象不經(jīng)過(guò)(　　) A．第一象限 B．第二象限 C．第三象限 D．第四象限 4．[2017·畢節(jié)]把直線y＝2x－1向左平移1個(gè)單位，平移后直線的關(guān)系式為(　　) A．y＝2x－2 B．y＝2x＋1 C．y＝2x

2、D．y＝2x＋2 5．[2017·陜西]若一個(gè)正比例函數(shù)的圖象經(jīng)過(guò)A(3，－6)，B(m，－4)兩點(diǎn)，則m的值為(　　) A．2 B．8 C．－2 D．－8 6．[2016·玉林]關(guān)于直線l：y＝kx＋k(k≠0)，下列說(shuō)法不正確的是(　　) A．點(diǎn)(0，k)在直線l上 B．直線l經(jīng)過(guò)定點(diǎn)(－1，0) C．當(dāng)k＞0時(shí)，y隨x的增大而增大 D．直線l經(jīng)過(guò)第一、二、三象限 圖K11－2 7．[2017·淄博]小明做了一個(gè)數(shù)學(xué)實(shí)驗(yàn)：將一個(gè)圓柱形的空玻璃杯放入形狀相同的無(wú)水魚(yú)缸內(nèi)，看作一個(gè)容器．然后，小明對(duì)準(zhǔn)玻璃杯口勻速注水，如圖K11－2所示，在注水過(guò)程中，杯底始終緊貼魚(yú)

3、缸底部．則下面可以近似地刻畫(huà)出容器最高水位h與注水時(shí)間t之間的變化情況的是(　　) 圖K11－3 8．[2017·齊齊哈爾]已知等腰三角形的周長(zhǎng)是10，底邊長(zhǎng)y是腰長(zhǎng)x的函數(shù)，則在圖K11－4所反映的圖象中，能正確反映y與x之間的函數(shù)關(guān)系的圖象是(　　) 圖K11－4 9．[2017·資陽(yáng)]若一次函數(shù)y＝mx＋n(m≠0)中的m，n是使等式m＝成立的整數(shù)，則一次函數(shù)y＝mx＋n(m≠0)的圖象一定經(jīng)過(guò)的象限是(　　) A．一、三 B．三、四 C．一、二 D．二、四 二、填空題 10．[2017·天津]若正比例函數(shù)y＝kx(k是常數(shù)，k≠0)的圖象經(jīng)過(guò)第二

4、、第四象限，則k的值可以是________(寫(xiě)出一個(gè)即可)． 11．[2017·成都]如圖K11－5，正比例函數(shù)y1＝k1x和一次函數(shù)y2＝k2x＋b的圖象相交于點(diǎn)A(2，1)，當(dāng)x<2時(shí)，y1________y2.(填“>”或“<”) 圖K11－5 12．[2017·眉山]設(shè)點(diǎn)(－1，m)和點(diǎn)(，n)是直線y＝(k2－1)x＋b(0＜k＜1)上的兩個(gè)點(diǎn)，則m、n的大小關(guān)系為_(kāi)_______． 13．[2017·株洲]如圖K11－6，直線y＝x＋與x軸、y軸分別交于點(diǎn)A，B，當(dāng)直線繞點(diǎn)A按順時(shí)針?lè)较蛐D(zhuǎn)到與x軸重合時(shí)，點(diǎn)B的運(yùn)動(dòng)路徑長(zhǎng)度是________． 圖K11－6 三

5、、解答題 14．[2017·杭州]在平面直角坐標(biāo)系中，一次函數(shù)y＝kx＋b(k，b都是常數(shù)，且k≠0)的圖象經(jīng)過(guò)點(diǎn)(1，0)和(0，2)． (1)當(dāng)－2＜x≤3時(shí)，求y的取值范圍； (2)已知點(diǎn)P(m，n)在該函數(shù)的圖象上，且m－n＝4，求點(diǎn)P的坐標(biāo)． 15．[2016·懷化]已知一次函數(shù)y＝2x＋4. (1)在如圖K11－7所示的平面直角坐標(biāo)系中畫(huà)出函數(shù)的圖象； (2)求圖象與x軸的交點(diǎn)A的坐標(biāo)，與y軸的交點(diǎn)B的坐標(biāo)； (3)在(2)的條件下，求出△AOB的面積； (4)利用圖象直接寫(xiě)出當(dāng)y＜0時(shí)，x的取值范圍． 圖K11－7 |拓 展 提 升| 16．[2015·

6、衡陽(yáng)]如圖K11－8，△A1B1A2，△A2B2A3，△A3B3A4，…，△AnBnAn＋1都是等腰直角三角形，其中點(diǎn)A1，A2，…，An在x軸上，點(diǎn)B1，B2，…，Bn在直線y＝x上，若OA2＝1，則OA2015的長(zhǎng)為_(kāi)_______． 圖K11－8 17．如圖K11－9，已知直線y＝－x＋2與x軸、y軸分別交于點(diǎn)A和點(diǎn)B，另外已知直線y＝kx＋b(k≠0)經(jīng)過(guò)點(diǎn)C(1，0)，且把△AOB分成兩部分． (1)若△AOB被分成的兩部分面積相等，求k和b的值； (2)若△AOB被分成的兩部分面積比為1∶5，求k和b的值． 圖K11－9

7、 參考答案 1．A　2.C　 3．C　[解析] ∵k＜0，∴－k＞0，∴一次函數(shù)y＝kx－k的圖象經(jīng)過(guò)一、二、四象限，不經(jīng)過(guò)第三象限．故選C. 4．B　 5．A　[解析] 設(shè)這個(gè)正比例函數(shù)的解析式為y＝kx，將A(3，－6)代入可得k＝－2，即y＝－2x，再將B(m，－4)代入y＝－2x，可得m＝2.故選A. 6．D 7．D　[解析] 開(kāi)始水位慢慢上升，當(dāng)水由玻璃杯溢出時(shí)，容器內(nèi)最高水位保持不變，當(dāng)水位慢慢超過(guò)空玻璃杯的高度時(shí)，水位又緩慢上升，由于此時(shí)魚(yú)缸的底面積大于空玻璃杯的底面積，所以同樣的流速情況下，水位上升的速度要比剛開(kāi)始往空玻璃杯中注水時(shí)水面高度

8、上升得慢，故選D. 8．D　[解析] 由題意得y＝10－2x， ∵∴＜x＜5. ∴符合要求的圖象是D. 9．B　[解析] 依題意可知n＋2＝±1， ∴或 (1)當(dāng)m＝1，n＝－1時(shí)，直線y＝mx＋n經(jīng)過(guò)一、三、四象限； (2)當(dāng)m＝－1，n＝－3時(shí)，直線y＝mx＋n經(jīng)過(guò)二、三、四象限． 可見(jiàn)一次函數(shù)y＝mx＋n(m≠0)的圖象一定經(jīng)過(guò)三、四象限． 故選B. 10．－1(答案不唯一，只需小于0即可) 11．<　[解析] 由題意得點(diǎn)A的橫坐標(biāo)為2，所以當(dāng)x<2時(shí)，y1

9、＞n. 13.　[解析] 先求得直線與x軸，y軸的交點(diǎn)坐標(biāo)，A(－1，0)，B(0，)，所以tan∠BAO＝＝，所以∠BAO＝60°.又AB＝＝2，所以點(diǎn)B的運(yùn)動(dòng)路徑長(zhǎng)度是＝. 14．解：(1)由題意知y＝kx＋2， 因?yàn)閳D象過(guò)點(diǎn)(1，0)，∴0＝k＋2， 解得k＝－2，∴y＝－2x＋2. 當(dāng)x＝－2時(shí)，y＝6.當(dāng)x＝3時(shí)，y＝－4. ∵k＝－2<0，∴函數(shù)值y隨x的增大而減小， ∴－4≤y<6. (2)根據(jù)題意知 解得∴點(diǎn)P的坐標(biāo)為(2，－2)． 15．解：(1)當(dāng)x＝0時(shí)，y＝4；當(dāng)y＝0時(shí)，x＝－2. ∴函數(shù)的圖象與兩坐標(biāo)軸的交點(diǎn)為A(－2，0)，B(0，4)．

10、根據(jù)“兩點(diǎn)確定一條直線”，由描點(diǎn)法作圖可得函數(shù)的圖象如下： (2)由(1)可知A(－2，0)，B(0，4)． (3)由(2)可得，OA＝2，OB＝4， ∴S△AOB＝·OA·OB＝×2×4＝4. (4)x＜－2. 16．22013　[解析] 因?yàn)镺A2＝1，所以可得OA1＝，進(jìn)而得出OA3＝2，OA4＝4，OA5＝8，由此得出OAn＝2n－2，所以O(shè)A2015＝22013. 17．解：(1)由題意知：A(2，0)，B(0，2)，直線y＝kx＋b(k≠0)經(jīng)過(guò)點(diǎn)C(1，0)，∴C是OA的中點(diǎn)， ∴直線y＝kx＋b一定經(jīng)過(guò)點(diǎn)B，C，把B，C的坐標(biāo)代入可得：解得 (2)∵S△AOB＝×2×2＝2，△AOB被分成的兩部分面積比為1∶5，所以直線y＝kx＋b(k≠0)與y軸或直線AB交點(diǎn)的縱坐標(biāo)就應(yīng)該是：2×2×＝，當(dāng)直線y＝kx＋b(k≠0)與直線y＝－x＋2相交時(shí)：當(dāng)y＝時(shí)，直線y＝－x＋2與y＝kx＋b(k≠0)的交點(diǎn)的橫坐標(biāo)就應(yīng)該滿足－x＋2＝，∴x＝，即交點(diǎn)的坐標(biāo)為(，)，又根據(jù)C點(diǎn)的坐標(biāo)為(1，0)，可得： ∴ 當(dāng)直線y＝kx＋b(k≠0)與y軸相交時(shí)，交點(diǎn)的坐標(biāo)就應(yīng)該是(0，)，又由C點(diǎn)的坐標(biāo)為(1，0)，可得： ∴因此：k＝2，b＝－2或k＝－，b＝. 5