《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問(wèn)題突破 專(zhuān)題6 方案設(shè)計(jì)題專(zhuān)題提升演練 新人教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計(jì) 第二板塊 熱點(diǎn)問(wèn)題突破 專(zhuān)題6 方案設(shè)計(jì)題專(zhuān)題提升演練 新人教版（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

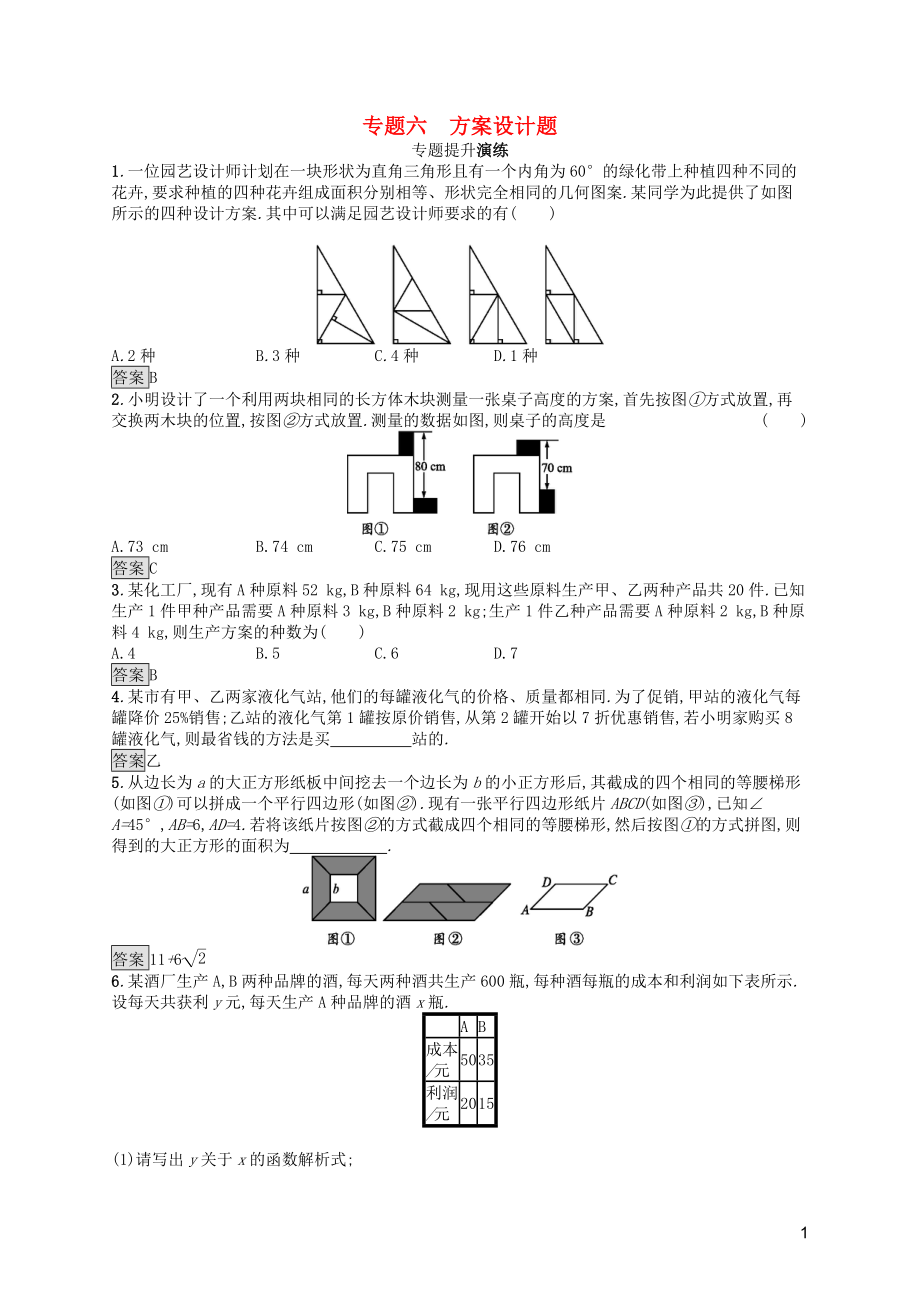
1、專(zhuān)題六　方案設(shè)計(jì)題 專(zhuān)題提升演練 1.一位園藝設(shè)計(jì)師計(jì)劃在一塊形狀為直角三角形且有一個(gè)內(nèi)角為60°的綠化帶上種植四種不同的花卉,要求種植的四種花卉組成面積分別相等、形狀完全相同的幾何圖案.某同學(xué)為此提供了如圖所示的四種設(shè)計(jì)方案.其中可以滿足園藝設(shè)計(jì)師要求的有(　　) 　　　　　　　　　　　　　　　　 A.2種 B.3種 C.4種 D.1種 答案B 2.小明設(shè)計(jì)了一個(gè)利用兩塊相同的長(zhǎng)方體木塊測(cè)量一張桌子高度的方案,首先按圖①方式放置,再交換兩木塊的位置,按圖②方式放置.測(cè)量的數(shù)據(jù)如圖,則桌子的高度是(　　) A.73 cm B.74 cm C.75 cm D.76 cm

2、答案C 3.某化工廠,現(xiàn)有A種原料52 kg,B種原料64 kg,現(xiàn)用這些原料生產(chǎn)甲、乙兩種產(chǎn)品共20件.已知生產(chǎn)1件甲種產(chǎn)品需要A種原料3 kg,B種原料2 kg;生產(chǎn)1件乙種產(chǎn)品需要A種原料2 kg,B種原料4 kg,則生產(chǎn)方案的種數(shù)為(　　) A.4 B.5 C.6 D.7 答案B 4.某市有甲、乙兩家液化氣站,他們的每罐液化氣的價(jià)格、質(zhì)量都相同.為了促銷(xiāo),甲站的液化氣每罐降價(jià)25%銷(xiāo)售;乙站的液化氣第1罐按原價(jià)銷(xiāo)售,從第2罐開(kāi)始以7折優(yōu)惠銷(xiāo)售,若小明家購(gòu)買(mǎi)8罐液化氣,則最省錢(qián)的方法是買(mǎi)　　　　　站的.? 答案乙 5.從邊長(zhǎng)為a的大正方形紙板中間挖去一個(gè)邊長(zhǎng)為b的小正方形后,

3、其截成的四個(gè)相同的等腰梯形(如圖①)可以拼成一個(gè)平行四邊形(如圖②).現(xiàn)有一張平行四邊形紙片ABCD(如圖③),已知∠A=45°,AB=6,AD=4.若將該紙片按圖②的方式截成四個(gè)相同的等腰梯形,然后按圖①的方式拼圖,則得到的大正方形的面積為　　　　　　.? 答案11+62 6.某酒廠生產(chǎn)A,B兩種品牌的酒,每天兩種酒共生產(chǎn)600瓶,每種酒每瓶的成本和利潤(rùn)如下表所示.設(shè)每天共獲利y元,每天生產(chǎn)A種品牌的酒x瓶. A B 成本/元 50 35 利潤(rùn)/元 20 15 (1)請(qǐng)寫(xiě)出y關(guān)于x的函數(shù)解析式; (2)如果該廠每天至少投入成本25 000元,且生產(chǎn)B種品牌

4、的酒不少于全天產(chǎn)量的55%,那么共有幾種生產(chǎn)方案?求出每天至少獲利多少元. 解(1)由題意,知每天生產(chǎn)B種品牌的酒(600-x)瓶,所以y=20x+15(600-x)=9000+5x. (2)根據(jù)題意得600-x≥600×55%,50x+35(600-x)≥25000, 解得26623≤x≤270, ∵x為整數(shù), ∴x的值可取267,268,269,270, 該酒廠共有4種生產(chǎn)方案: ①生產(chǎn)A種品牌的酒267瓶,B種品牌的酒333瓶; ②生產(chǎn)A種品牌的酒268瓶,B種品牌的酒332瓶; ③生產(chǎn)A種品牌的酒269瓶,B種品牌的酒331瓶; ④生產(chǎn)A種品牌的酒270瓶,B種品牌

5、的酒330瓶. ∵y=9000+5x,y是關(guān)于x的一次函數(shù),且y隨x的增大而增大, ∴當(dāng)x=267時(shí),y有最小值,y最小=9000+5×267=10335. ∴該酒廠共有4種生產(chǎn)方案,每天至少獲利10335元. 7.木匠黃師傅用長(zhǎng)AB=3,寬BC=2的矩形木板做一個(gè)盡可能大的圓形桌面,他設(shè)計(jì)了四種方案: 方案一:直接鋸一個(gè)半徑最大的圓; 方案二:圓心O1,O2分別在CD,AB上,半徑分別是O1C,O2A,鋸兩個(gè)外切的半圓拼成一個(gè)圓; 方案三:沿對(duì)角線AC將矩形鋸成兩個(gè)三角形,適當(dāng)平移三角形并鋸一個(gè)最大的圓; 方案四:鋸一塊小矩形BCEF拼到矩形AFED下面,利用拼成的木板鋸一個(gè)

6、盡可能大的圓. (1)寫(xiě)出方案一中圓的半徑; (2)通過(guò)計(jì)算說(shuō)明方案二和方案三中,哪個(gè)圓的半徑較大; (3)在方案四中,設(shè)CE=x(0