《2019-2020學(xué)年高中物理 第3章 磁場 習(xí)題課4 帶電粒子在磁場或復(fù)合場中的運動學(xué)案 粵教版選修3-1》由會員分享，可在線閱讀，更多相關(guān)《2019-2020學(xué)年高中物理 第3章 磁場 習(xí)題課4 帶電粒子在磁場或復(fù)合場中的運動學(xué)案 粵教版選修3-1（11頁珍藏版）》請在裝配圖網(wǎng)上搜索。

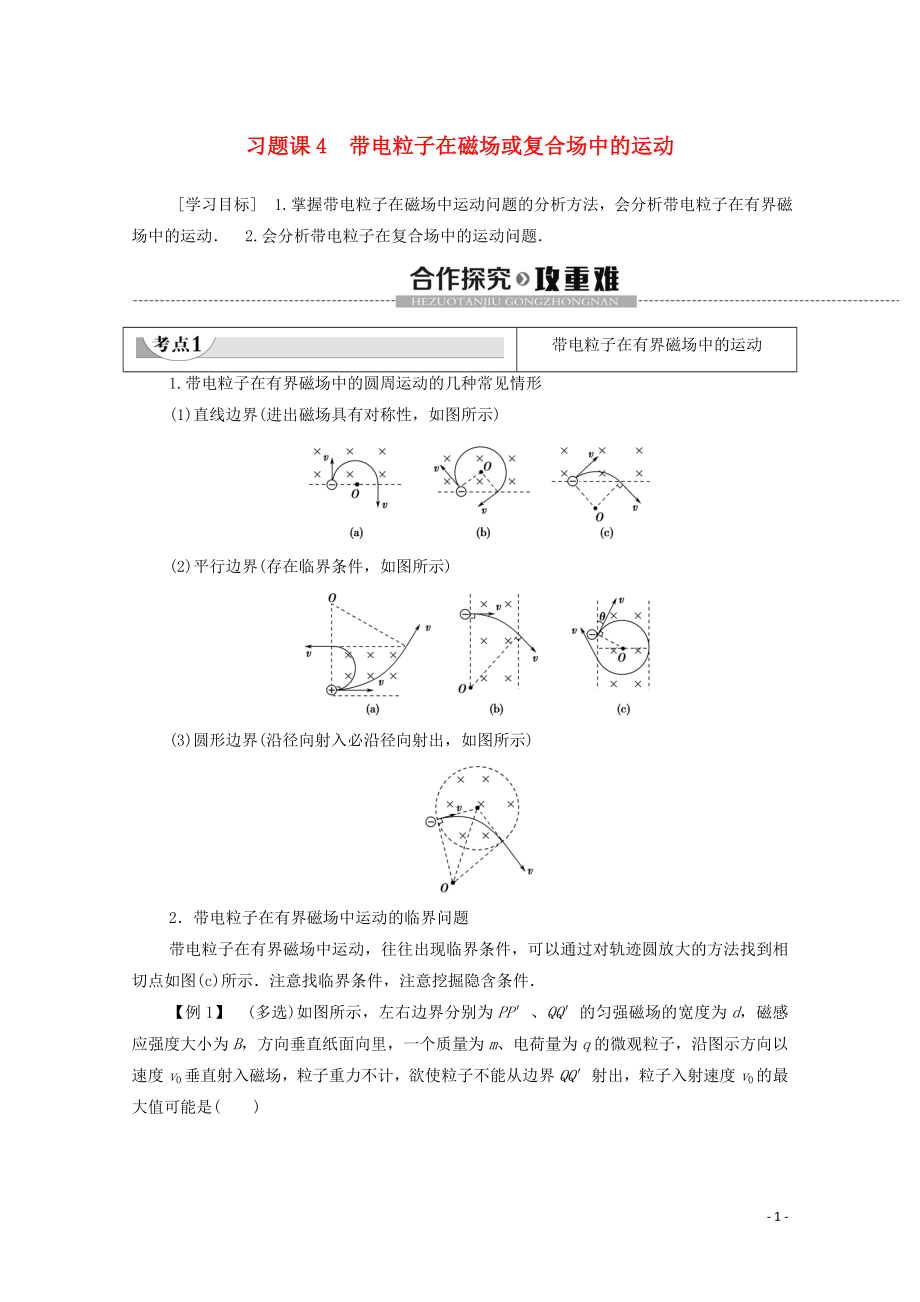
1、習(xí)題課4　帶電粒子在磁場或復(fù)合場中的運動 [學(xué)習(xí)目標(biāo)]　1.掌握帶電粒子在磁場中運動問題的分析方法，會分析帶電粒子在有界磁場中的運動．　2.會分析帶電粒子在復(fù)合場中的運動問題． 帶電粒子在有界磁場中的運動 1.帶電粒子在有界磁場中的圓周運動的幾種常見情形 (1)直線邊界(進出磁場具有對稱性，如圖所示) (2)平行邊界(存在臨界條件，如圖所示) (3)圓形邊界(沿徑向射入必沿徑向射出，如圖所示) 2．帶電粒子在有界磁場中運動的臨界問題 帶電粒子在有界磁場中運動，往往出現(xiàn)臨界條件，可以通過對軌跡圓放大的方法找到相切點如圖(c)所示．注意找臨界條件，注意挖掘隱含

2、條件． 【例1】　(多選)如圖所示，左右邊界分別為PP′、QQ′的勻強磁場的寬度為d，磁感應(yīng)強度大小為B，方向垂直紙面向里，一個質(zhì)量為m、電荷量為q的微觀粒子，沿圖示方向以速度v0垂直射入磁場，粒子重力不計，欲使粒子不能從邊界QQ′射出，粒子入射速度v0的最大值可能是(　　) A．　 B． C． D． BC　[粒子射入磁場后做勻速圓周運動，由R＝知，粒子的入射速度v0越大，R越大，當(dāng)粒子的徑跡和邊界QQ′相切時，粒子剛好不從QQ′射出，此時其入射速度v0應(yīng)為最大，若粒子帶正電，其運動軌跡如圖甲所示(此時圓心為O點)，容易看出R1sin 45°＋d＝R1，將R1＝代入上式得v0＝，B

3、正確；若粒子帶負電，其運動徑跡如圖乙所示(此時圓心為O′點)，容易看出R2＋R2cos 45°＝d，將R2＝代入上式得v0＝，C正確． ] 1．如圖所示，在一邊長為d的正方形區(qū)域內(nèi)，存在垂直紙面向里的勻強磁場，一質(zhì)量為m、電荷量為＋q的帶電粒子從AB邊的中點O處以速度v0垂直AB邊進入磁場做圓周運動，則下列關(guān)于粒子運動的說法中正確的是(　　) A．若帶電粒子恰能從D點飛出磁場，則粒子作圓周運動的半徑應(yīng)為d B．若帶電粒子恰能從D點飛出磁場，則該勻強磁場的磁感應(yīng)強度應(yīng)為 C．若減小該勻強磁場的磁感應(yīng)強度B，則該帶電粒子在磁場中運動的時間將變長 D．若使帶電粒子進入磁場的初速度

4、v0增大，則粒子在該磁場中做圓周運動的周期也將變大 A　[粒子在磁場中做勻速圓周運動，若帶電粒子恰能從D點飛出磁場，其運動軌跡如圖所示． 設(shè)軌跡半徑為r，則有 d2＋(r－0.5d)2＝r2；則r＝d，故A正確．根據(jù)qv0B＝m得B＝＝，故B錯誤．若減小該勻強磁場的磁感應(yīng)強度B，由T＝知粒子圓周運動的周期T變大．由r＝知軌跡半徑變大，軌跡對應(yīng)的圓心角θ變小，根據(jù)t＝T知該帶電粒子在磁場中運動的時間不一定變長，故C錯誤．由T＝知粒子圓周運動的周期T與初速度無關(guān)，則知若使帶電粒子進入磁場的初速度v0增大，周期不變，故D錯誤．故選A.] 帶電粒子在組合場中的運動 　帶電粒子在電場、

5、磁場的組合場中的運動是指粒子從電場到磁場、或從磁場到電場的運動．通常按時間的先后順序分成若干個小過程，在每一運動過程中從粒子的受力性質(zhì)、受力方向和速度方向的關(guān)系入手，分析粒子在電場中做什么運動，在磁場中做什么運動． (1)在電場中運動 ①若初速度v0與電場線平行，粒子做勻變速直線運動； ②若初速度v0與電場線垂直，粒子做類平拋運動． (2)在磁場中運動 ①若初速度v0與磁感線平行，粒子做勻速直線運動； ②若初速度v0與磁感線垂直，粒子做勻速圓周運動． (3)解決帶電粒子在組合場中的運動問題，所需知識如下： 【例2】　一足夠長的條狀區(qū)域內(nèi)存在勻強電場和勻強磁場，其在xOy平面

6、內(nèi)的截面如圖所示：中間是磁場區(qū)域，其邊界與y軸垂直，寬度為l，磁感應(yīng)強度的大小為B，方向垂直于xOy平面；磁場的上、下兩側(cè)為電場區(qū)域，寬度均為l′，電場強度的大小均為E，方向均沿x軸正方向；M、N為條狀區(qū)域邊界上的兩點，它們的連線與y軸平行．一帶正電的粒子以某一速度從M點沿y軸正方向射入電場，經(jīng)過一段時間后恰好以從M點入射的速度從N點沿y軸正方向射出．不計重力． (1)定性畫出該粒子在電磁場中運動的軌跡； (2)求該粒子從M點入射時速度的大??； (3)若該粒子進入磁場時的速度方向恰好與x軸正方向的夾角為，求該粒子的比荷及其從M點運動到N點的時間． 思路點撥：(1)帶電粒子在電場中做

7、類平拋運動，在磁場中做勻速圓周運動． (2)帶電粒子在磁場中做勻速圓周運動的速度是從下方電場中射出的末速度． (3)因電場和磁場的分布具有對稱性，帶電粒子的運動軌跡也具有對稱性． 甲 [解析]　(1)粒子運動的軌跡如圖甲所示．(粒子在電場中的軌跡為拋物線，在磁場中為圓弧，上下對稱) (2)粒子從電場下邊界入射后在電場中做類平拋運動．設(shè)粒子從M點射入時速度的大小為v0，在下側(cè)電場中運動的時間為t，加速度的大小為a；粒子進入磁場的速度大小為v，方向與電場方向的夾角為θ(見圖乙)，速度沿電場方向的分量為v1.根據(jù)牛頓第二定律有 qE＝ma ① 乙 式中q和m分別為粒子的電荷量

8、和質(zhì)量．由運動學(xué)公式有 v1＝at ② l′＝v0t ③ v1＝vcos θ ④ 粒子在磁場中做勻速圓周運動，設(shè)其運動軌道半徑為R，由洛倫茲力公式和牛頓第二定律得 qvB＝m ⑤ 由幾何關(guān)系得 l＝2Rcos θ ⑥ 聯(lián)立①②③④⑤⑥式得 v0＝. ⑦ (3)由運動學(xué)公式和題給數(shù)據(jù)得 v1＝v0cot ⑧ 聯(lián)立①②③⑦⑧式得 ＝ ⑨ 設(shè)粒子由M點運動到N點所用的時間為t′，則 t′＝2t＋T ⑩ 式中T是粒子在磁場中做勻速圓周運動的周期． T＝ ? 由③⑦⑨⑩?式得 t′＝(1＋)． ? [答案]　(1)圖見解析　(2)　(3)　(1＋) “電

9、偏轉(zhuǎn)”與“磁偏轉(zhuǎn)”的比較 垂直電場線進入勻強電場(不計重力) 垂直磁感線進入勻強磁場(不計重力) 受力情況 電場力FE＝qE，其大小、方向不變，與速度v無關(guān)，F(xiàn)E是恒力 洛倫茲力FB＝qvB，其大小不變，方向隨v而改變，F(xiàn)B是變力 軌跡 拋物線 圓或圓的一部分 運動軌跡 求解方法 利用類平拋運動的規(guī)律求解vx＝v0，x＝v0t vy＝·t y＝··t2 偏轉(zhuǎn)角φ tan φ＝＝ 半徑r＝ 周期T＝ 偏移距離y和偏轉(zhuǎn)角φ要結(jié)合圓的幾何關(guān)系利用圓周運動規(guī)律討論求解 運動時間 t＝ t＝T＝ 2.如圖所示，兩導(dǎo)體板水平放置，兩板間電勢差為U

10、，帶電粒子以某一初速度v0沿平行于兩板的方向從兩板正中間射入，穿過兩板后又垂直于磁場方向射入邊界線豎直的勻強磁場(不計重力)，則粒子射入磁場和射出磁場的M、N兩點間的距離d隨著U和v0的變化情況有(　　) A．d隨v0增大而增大，d與U無關(guān) B．d隨v0增大而增大，d隨U增大而增大 C．d隨U增大而增大，d與v0無關(guān) D．d隨v0增大而增大，d隨U增大而減小 A　[設(shè)帶電粒子射出電場時速度的偏轉(zhuǎn)角為θ，如圖所示，有cos θ＝，又R＝，而d＝2Rcos θ＝2cos θ＝，A正確． ] 帶電粒子在疊加場中的運動 1.帶電粒子在疊加場中的運動一般有兩種情況： (1)直線

11、運動：如果帶電粒子在疊加場中做直線運動，一定是做勻速直線運動，合力為零． (2)圓周運動：如果帶電粒子在疊加場中做圓周運動，一定是做勻速圓周運動，重力和電場力的合力為零，洛倫茲力提供向心力． 2．處理帶電粒子在疊加場中的運動問題的基本思路 (1)弄清疊加場的組成． (2)進行受力分析，確定帶電粒子的運動狀態(tài)，注意運動情況和受力情況的結(jié)合． (3)畫出粒子運動軌跡，靈活選擇不同的運動規(guī)律． ①當(dāng)帶電粒子在疊加場中做勻速直線運動時，根據(jù)受力平衡列方程求解． ②當(dāng)帶電粒子在疊加場中做勻速圓周運動時，一定是電場力和重力平衡，洛倫茲力提供向心力，應(yīng)用平衡條件和牛頓運動定律分別列方程求解．

12、 ③當(dāng)帶電粒子做復(fù)雜曲線運動時，一般用動能定理或能量守恒定律求解． 【例3】　如圖所示，兩塊相同的金屬板MN、PQ平行傾斜放置，與水平面的夾角為45°，兩金屬板間的電勢差為U，PQ板電勢高于MN板，且MN、PQ之間分布有方向與紙面垂直的勻強磁場．一質(zhì)量為m、帶電量為q的小球從PQ板的P端以速度v0豎直向上射入，恰好沿直線從MN板的N端射出，重力加速度為g，求： (1)磁感應(yīng)強度的大小和方向； (2)小球在金屬板之間的運動時間． [解析]　(1)小球在金屬板之間只能做勻速直線運動，受重力G，電場力F電和洛倫茲力f，F(xiàn)電的方向與金屬板垂直，由左手定則可知f的方向沿水平方向，受力如圖，三

13、力合力為零，故小球帶正電，金屬板MN、PQ之間的磁場方向垂直紙面向外，其中qv0B＝mgtan θ 可得B＝. (2)小球在運動的過程中由于洛倫茲力不做功，只有電場力與重力做功，設(shè)NP之間的高度為h，則由動能定理可得qU－mgh＝0－0， 又h＝v0t， 解得t＝. [答案]　(1)　垂直紙面向外　(2) 3．如圖所示，空間存在豎直向上的勻強電場和水平的勻強磁場(垂直紙面向里)．一帶正電小球從O點靜止釋放后，運動軌跡為圖中OPQ所示，其中P為運動軌跡中的最高點，Q為與O同一水平高度的點．下列關(guān)于該帶電小球運動的描述，正確的是(　　) A．小球在運動過程中受到的磁場力先增大

14、后減小 B．小球在運動過程中電勢能先增加后減少 C．小球在運動過程中機械能守恒 D．小球到Q點后將沿著QPO軌跡回到O點 A　[小球由靜止開始運動，可知電場力大于重力，在運動的過程中，洛倫茲力不做功，電場力和重力的合力先做正功，后做負功，根據(jù)動能定理知，小球的速度先增大后減小，則小球受到的磁場力先增大后減小，故A正確．小球在運動的過程中，電場力先做正功，再做負功，則電勢能先減小后增加，故B錯誤．小球在運動的過程中，除重力做功以外，電場力也做功，機械能不守恒，故C錯誤．小球到Q點后，有可能重復(fù)之前的運動，不會沿著QPO軌跡回到O點，故D錯誤．] 1．(多選)在如圖所示的勻強電場和勻

15、強磁場共存的區(qū)域內(nèi)電子可能沿水平方向向右做直線運動的是(　　) BC　[由力與運動的關(guān)系可知，電子若向右做直線運動，所受合外力的方向或向左，或向右，或合外力為零．A項中，電子受到的電場力向左，洛倫茲力向下，A錯；B項中，電子不受洛倫茲力，電場力向左，B對；C項中，電子受到的電場力向上，洛倫茲力向下，如果兩力平衡，符合題意，C對；D項中，電子受到的電場力和洛倫茲力都向上，D錯．] 2.如圖，半徑為R的半圓形區(qū)域內(nèi)有垂直于紙面向外的勻強磁場．一質(zhì)量為m、帶電量為＋q且不計重力的粒子，以速度v沿與半徑PO夾角θ＝30°的方向從P點垂直磁場射入，最后粒子垂直于MN射出，則磁感應(yīng)強度的大小為(　

16、　) A． B．　　　C.　　　D. B　[粒子在磁場中做勻速圓周運動，洛倫茲力提供向心力，運動軌跡如圖，由幾何關(guān)系，知圓心角30°，粒子運動的軌跡的半徑為r＝2R① 根據(jù)洛倫茲力提供向心力，有qvB＝m得半徑為r＝② 聯(lián)立①②得B＝，故B正確，A、C、D錯誤．] 3．(多選)一個帶電粒子以初速度v0垂直于電場方向向右射入勻強電場區(qū)域，穿出電場后接著又進入勻強磁場區(qū)域．設(shè)電場和磁場區(qū)域有明確的分界線，且分界線與電場強度方向平行，如圖中的虛線所示．在圖所示的幾種情況中，可能出現(xiàn)的是(　　) AD　[A、C選項中粒子在電場中向下偏轉(zhuǎn)，所以粒子帶正電，再進入磁場后，A圖

17、中粒子應(yīng)逆時針轉(zhuǎn)，正確；C圖中粒子應(yīng)順時針轉(zhuǎn)，錯誤．同理可以判斷B錯，D對．] 4.已知質(zhì)量為m的帶電液滴，以速度v射入互相垂直的勻強電場E和勻強磁場B中，液滴在此空間剛好能在豎直平面內(nèi)做勻速圓周運動．如圖所示．求： (1)液滴在空間受幾個力作用？ (2)液滴帶電荷量及電性． (3)液滴做勻速圓周運動的半徑多大？ [解析]　(1)由于是帶電液滴，它必然受重力，又處于電、磁場中，還應(yīng)受到電場力及洛倫茲力，共三個力作用．(2)因液滴做勻速圓周運動，故必須滿足重力與電場力平衡，所以液滴應(yīng)帶負電，電荷量由mg＝Eq，求得：q＝.(3)液滴做圓周運動的向心力由洛倫茲力提供，由牛頓第二定律qvB＝m，所以半徑r＝，把電荷量代入可得：r＝＝. [答案]　(1)三個　(2)　負電　(3) - 11 -