《（名師導學）2020版高考數(shù)學總復習 第三章 導數(shù)及其應用 第15講 導數(shù)的概念及運算練習 文（含解析）新人教A版》由會員分享，可在線閱讀，更多相關《（名師導學）2020版高考數(shù)學總復習 第三章 導數(shù)及其應用 第15講 導數(shù)的概念及運算練習 文（含解析）新人教A版（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。

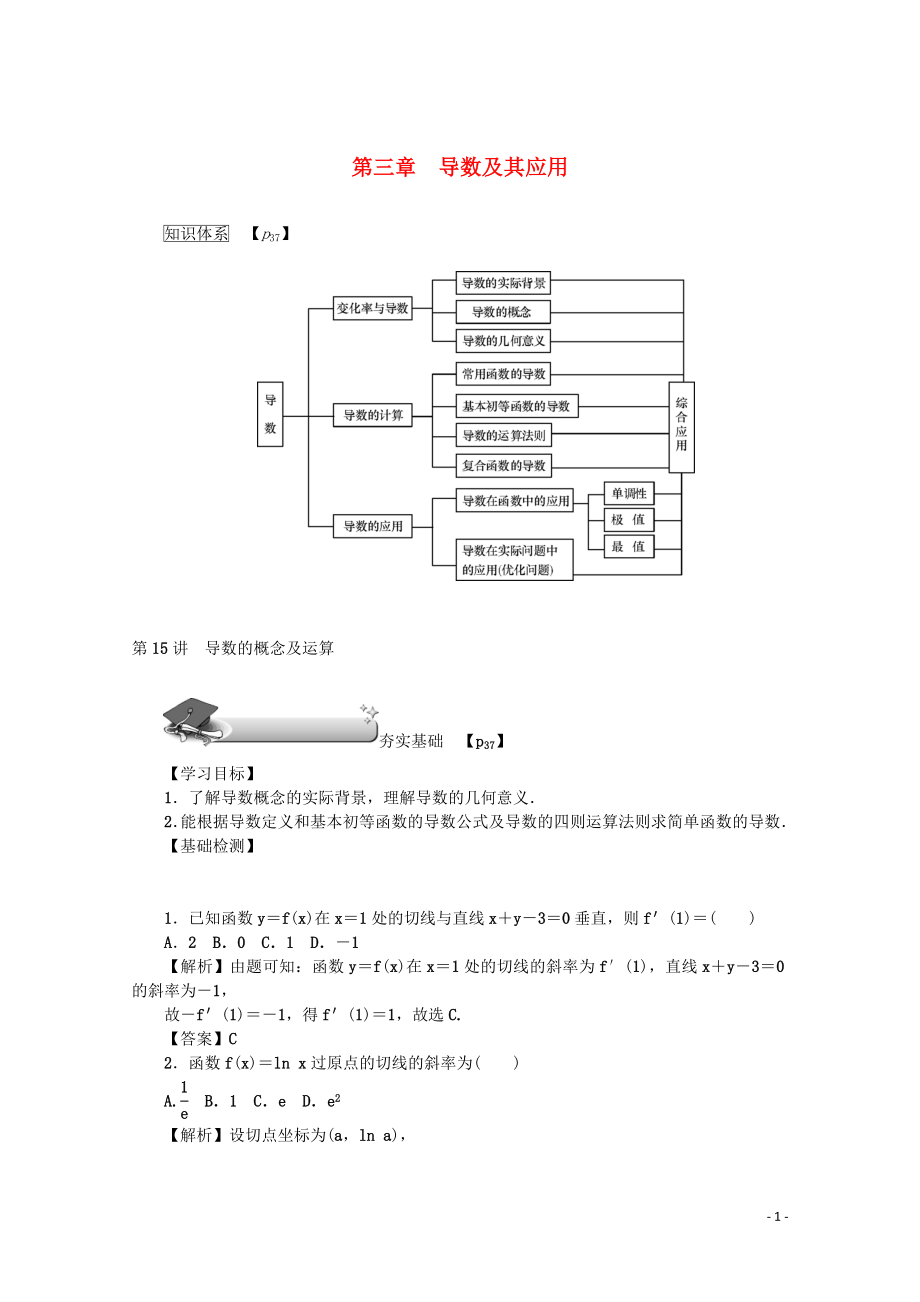
1、第三章　導數(shù)及其應用 　【p37】 第15講　導數(shù)的概念及運算 夯實基礎　【p37】 【學習目標】 1．了解導數(shù)概念的實際背景，理解導數(shù)的幾何意義． 2．能根據(jù)導數(shù)定義和基本初等函數(shù)的導數(shù)公式及導數(shù)的四則運算法則求簡單函數(shù)的導數(shù)． 【基礎檢測】 　　　　　　　　　　　　　　　　　　　 1．已知函數(shù)y＝f(x)在x＝1處的切線與直線x＋y－3＝0垂直，則f′(1)＝(　　) A．2 B．0 C．1 D．－1 【解析】由題可知：函數(shù)y＝f(x)在x＝1處的切線的斜率為f′(1)，直線x＋y－3＝0的斜率為－1， 故－f′(1)＝－1，得f′(1)＝1，

2、故選C. 【答案】C 2．函數(shù)f(x)＝ln x過原點的切線的斜率為(　　) A. B．1 C．e D．e2 【解析】設切點坐標為(a，ln a)， ∵y＝ln x，∴y′＝， 切線的斜率是， 切線的方程為y－ln a＝(x－a)， 將(0，0)代入可得ln a＝1，∴a＝e， ∴切線的斜率是＝. 故選A. 【答案】A 3．曲線y＝－5ex＋3在點(0，－2)處的切線方程為__________． 【解析】y′＝－5ex， 又點(0，－2)在曲線上， 所以y′|x＝0＝－5， 切線方程為y－(－2)＝－5(x－0)， 即y＋5x＋2＝0. 【答案】y＋5

3、x＋2＝0 4．直線y＝kx＋1與曲線y＝x3＋ax＋b相切于點A(1，3)，則b的值為__________． 【解析】由切點可知k＋1＝3，1＋a＋b＝3.對曲線方程求導可得y′＝3x2＋a，可知3＋a＝k，解方程組可得b＝3. 【答案】3 【知識要點】 1．導數(shù)的概念 (1)函數(shù)y＝f(x)在x＝x0處的導數(shù) 函數(shù)y＝f(x)在x＝x0處的瞬時變化率： lim ＝lim 為函數(shù)y＝f(x)在x＝x0處的導數(shù)，記作f′(x0)或y′|x＝x0，即f′(x0)＝lim ＝lim ____. (2)導數(shù)的幾何意義 函數(shù)f(x)在點x0處的導數(shù)f′(x0)的幾何意義是在曲線

4、y＝f(x)上點__P(x0，y0)__處的__切線的斜率__(瞬時速度就是位移函數(shù)s(t)對時間t的導數(shù))．相應地，切線方程為__y－y0＝f′(x0)(x－x0)__． (3)函數(shù)f(x)的導函數(shù) 稱函數(shù)f′(x)＝lim 為f(x)的導函數(shù)． 2．基本初等函數(shù)的導數(shù)公式 (xn)′＝__nxn－1__，(sin x)′＝__cos____x__， (cos x)′＝__－sin__x__，(ax)′＝__axln__a__， (ex)′＝__ex__，(logax)′＝____，(ln x)′＝. 3．導數(shù)的運算法則 (1)[f(x)±g(x)]′＝__f′(x)±g′(

5、x)__； (2)[f(x)·g(x)]′＝__f′(x)g(x)＋f(x)g′(x)__； (3)′＝(g(x)≠0)． 典 例 剖 析　【p38】 考點1　導數(shù)的計算 求下列函數(shù)的導數(shù)： (1)y＝5x2－4x＋1； (2)y＝(2x2－1)(3x＋1)； (3)y＝(x≠0)； (4)y＝. 【解析】(1)y′＝10x－4； (2)y′＝4x·(3x＋1)＋(2x2－1)·3＝18x2＋4x－3； (3)y′＝＝； (4)y′＝′＝(cos x－sin x)′ ＝－sin x－cos x. 【小結】函數(shù)求導的基本步驟： 1．求導之前，應利用代數(shù)、三角恒等式

6、等變形對函數(shù)進行化簡，然后求導； 2．準確地把函數(shù)分割為能用求導公式的函數(shù)的和、差、積、商； 3．再利用運算法則求導數(shù)并整理結果． 考點2　導數(shù)的幾何意義 (1)曲線y＝ex在點A處的切線與直線x－y＋3＝0平行，則點A的坐標為(　　) A．(－1，e－1 ) B．(0，1) C．(1，e) D．(0，2) 【解析】設A(x0，ex0)，y′＝ex，所以切線斜率為ex0＝1，x0＝0，所以A(0，1)．故選B. 【答案】B (2)曲線y＝x(3ln x＋1)在第(1，1)處的切線方程為________________． 【解析】對曲線求導可得， y′＝f′(x)＝3l

7、n x＋1＋x·＝3ln x＋4， 故f′(1)＝4， 則切線方程為y－1＝4(x－1)， 整理得y＝4x－3. 【答案】y＝4x－3 【小結】曲線y＝f(x)在點P(x0，f(x0))處的切線方程是y－f(x0)＝f′(x0)(x－x0)． 考點3　導數(shù)運算的應用 (1)已知函數(shù)f＝ex－ln x，則函數(shù)在點處的切線與兩坐標軸圍成的三角形的面積為__________． 【解析】由題，x∈，又f′＝ex－， 則切線的斜率k＝f′＝e－1， 又點在曲線上，則f＝e，切點的坐標為. 可得切線的方程為y－e＝， 當x＝0時， y＝1，當y＝0時，x＝， 切線與兩坐標軸圍成的

8、三角形的面積為S＝×1×＝. 【答案】 (2)已知M，N分別是曲線y＝ex與直線y＝ex－1上的點，則線段MN的最小值為______________． 【解析】設曲線y＝ex在某點處的切線為l，當切線l與直線y＝ex－1平行時，這兩條平行直線間的距離就是所求的最小值． 因為切線l與直線y＝ex－1平行，所以切線l的斜率為e. 設切點為M(a，b)， 又曲線y＝ex在點M(a，b)處的切線的斜率為y′|x＝a＝ea， 所以ea＝e，得a＝1，所以切點M的坐標為(1，e)， 故切線l的方程為y－e＝e(x－1)，即ex－y＝0. 又直線y＝ex－1，即ex－y－1＝0， 所以d

9、＝＝，即線段MN的最小值為. 【答案】 【能力提升】 已知函數(shù)f(x)＝ln x＋(a∈R)． (1)若函數(shù)f(x)在區(qū)間(0，4)上單調(diào)遞增，求a的取值范圍； (2)若函數(shù)y＝f(x)的圖象與直線y＝2x相切，求a的值． 【解析】(1)f′(x)＝＋＝， ∵函數(shù)f(x)在區(qū)間(0，4)上單調(diào)遞增， ∴f′(x)≥0在(0，4)上恒成立， ∴(x＋1)2＋ax≥0， 即a≥－在(0，4)上恒成立， ∵x＋≥2，取等號條件為當且僅當x＝1， ∴a≥－4. (2)設切點為(x0，y0)， 則y0＝2x0，f′(x0)＝2，y0＝ln x0＋， ∴＋＝2，　① 且2x

10、0＝ln x0＋，?、? 由①得a＝(x0＋1)2，代入②得 2x0＝ln x0＋(2x0－1)(x0＋1)， 即ln x0＋2x－x0－1＝0. 令F(x)＝ln x＋2x2－x－1， 則F′(x)＝＋4x－1＝， ∵方程4x2－x＋1＝0的Δ＝－15<0， ∴4x2－x＋1>0恒成立． ∴F′(x)在(0，＋∞)上恒為正值， ∴F(x)在(0，＋∞)上單調(diào)遞增， ∵F(1)＝0，∴x0＝1，代入①式得a＝4. 【小結】x＝x0處的導數(shù)值就是該點處的切線的斜率是解決有關切線問題的關鍵． 方 法 總 結　【p38】 1．掌握基本初等函數(shù)的導數(shù)公式和導數(shù)的四則運算法則．

11、 2．導數(shù)的幾何意義是高考考查的熱點問題，應特別注意“過點P的切線”與“在點P處的切線”意義完全不一樣，前者點P不一定是切點，而后者點P一定是切點，且在曲線上． 走 進 高 考　　【p38】 1．(2018·天津)已知函數(shù)f(x)＝exln x，f′(x)為f(x)的導函數(shù)，則f′(1)的值為________． 【解析】由題意得f′(x)＝exln x＋ex·，則f′(1)＝e. 【答案】e 2．(2018·全國卷Ⅰ)設函數(shù)f(x)＝x3＋(a－1)x2＋ax.若f(x)為奇函數(shù)，則曲線y＝f(x)在點(0，0)處的切線方程為(　　) A．y＝－2x B．y＝－x C．y＝2x D．y＝x 【解析】因為f(x)為奇函數(shù)，所以f(－x)＝－f(x)，由此可得a＝1，故f(x)＝x3＋x，f′(x)＝3x2＋1，f′(0)＝1，所以曲線y＝f(x)在點(0，0)處的切線方程為y＝x. 【答案】D - 6 -