《2015高中數(shù)學 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3》由會員分享，可在線閱讀，更多相關(guān)《2015高中數(shù)學 2.3變量間的相關(guān)關(guān)系講解 新人教A版必修3（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、2. 3變量間的相關(guān)關(guān)系(講) 一、相關(guān)關(guān)系： 自變量取值一定時，因變量的取值帶有一定隨機性的兩個變量之間的關(guān)系，叫做相關(guān)關(guān)系。 【說明】函數(shù)關(guān)系是一種非常確定的關(guān)系，而相關(guān)關(guān)系是一種非確定性關(guān)系。 思考探究： 1、有關(guān)法律規(guī)定，香煙盒上必須印上“吸煙有害健康”的警示語。吸煙是否一定會引起健康問題？你認為“健康問題不一定是由吸煙引起的，所以可以吸煙”的說法對嗎？ 2、某地區(qū)的環(huán)境條件適合天鵝棲息繁衍，有人經(jīng)統(tǒng)計發(fā)現(xiàn)了一個有趣的現(xiàn)象，如果村莊附近棲息的天鵝多，那么這個村莊的嬰兒出生率也高，天鵝少的地方嬰兒出生率低，于是他得出了一個結(jié)論：天鵝能夠帶來孩子。你認為這樣的結(jié)論可靠嗎？如何證

2、明這個問題的可靠性？ 分析：（1）吸煙只是影響健康的一個因素，對健康的影響還有其他的一些因素，兩者之間非函數(shù)關(guān)系即非因果關(guān)系； （2）不對，這也是相關(guān)關(guān)系而不是函數(shù)關(guān)系。 上面提到了很多相關(guān)關(guān)系，那它們之間的相關(guān)關(guān)系強還是弱？我們下面來研究一下。 二、散點圖 探究：在一次對人體脂肪含量和年齡關(guān)系的研究中，研究人員獲得了一組樣本數(shù)據(jù)： 年齡 23 27 39 41 45 49 50 脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2

3、 年齡 53 54 56 57 58 60 61 脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6 其中各年齡對應的脂肪數(shù)據(jù)是這個年齡人群脂肪含量的樣本平均數(shù)。 思考探究： 1、對某一個人來說，他的體內(nèi)脂肪含量不一定隨年齡增長而增加或減少，但是如果把很多個體放在一起，就可能

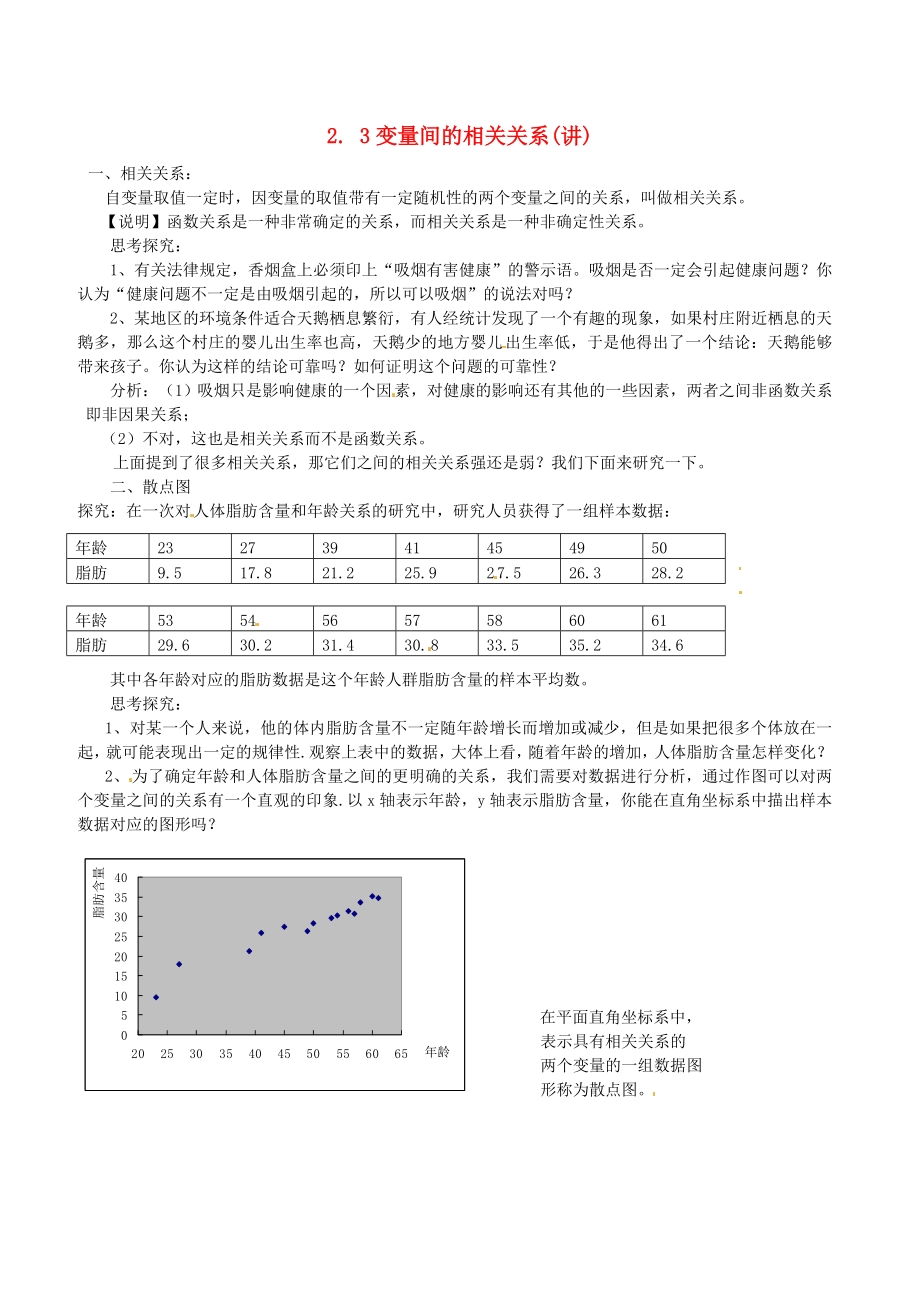
4、表現(xiàn)出一定的規(guī)律性.觀察上表中的數(shù)據(jù)，大體上看，隨著年齡的增加，人體脂肪含量怎樣變化？ 2、為了確定年齡和人體脂肪含量之間的更明確的關(guān)系，我們需要對數(shù)據(jù)進行分析，通過作圖可以對兩個變量之間的關(guān)系有一個直觀的印象.以x軸表示年齡，y軸表示脂肪含量，你能在直角坐標系中描出樣本數(shù)據(jù)對應的圖形嗎？ 在平面直角坐標系中， 表示具有相關(guān)關(guān)系的 兩個變量的一組數(shù)據(jù)圖 形稱為散點圖。 3、觀察人的年齡的與人體脂肪含量散點圖

5、的大致趨勢，有什么樣的特點？閱讀課本，這種相關(guān)關(guān)系我們稱為什么？還有沒有其他的相關(guān)關(guān)系？它又有怎樣的特點？ 三、線性相關(guān)、回歸直線方程和最小二乘法 在各種各樣的散點圖中，有些散點圖中的點是雜亂分布的，有些散點圖中的點的分布有一定的規(guī)律性，年齡和人體脂肪含量的樣本數(shù)據(jù)的散點圖中的點的分布有什么特點？ 如果散點圖中的點的分布，從整體上看大致在一條直線附近，則稱這兩個變量之間具有線性相關(guān)關(guān)系，這條直線叫做回歸直線。 我們所畫的回歸直線應該使散點圖中的各點在整體上盡可能的與其接近。我們怎么來實現(xiàn)這一目的呢？說一說你的想法。 設所求的直線方程為=bx+a，其中a、b是待定系數(shù)。 則i=bx

6、i+a（i=1，2，…，n）.于是得到各個偏差 yi－i =yi－（bxi+a）（i=1，2，…，n） 顯見，偏差yi－i 的符號有正有負，若將它們相加會造成相互抵消，所以它們的和不能代表幾個點與相應直線在整體上的接近程度，故采用n個偏差的平方和 Q=（y1－bx1－a）2+（y2－bx2－a）2+…+（yn－bxn－a）2 表示n個點與相應直線在整體上的接近程度。 記Q= 這樣，問題就歸結(jié)為：當a、b取什么值時Q最小，a、b的值由下面的公式給出： 其中=，=，a為回歸方程的斜率，b為截距。 求回歸直線，使得樣本數(shù)據(jù)的點到它的距離的平方和最小的方法叫最小二乘法。 【例題精

7、析】 有一個同學家開了一個小賣部，他為了研究氣溫對熱飲銷售的影響，經(jīng)過統(tǒng)計，得到一個賣出的飲料杯數(shù)與當天氣溫的對比表： 攝氏溫度 -5 0 4 7 12 15 19 23 27 31 36 熱飲杯數(shù) 156 150 132 128 130 116 104 89 93 76 54 （1）畫出散點圖； （2）從散點圖中發(fā)現(xiàn)氣溫與熱飲杯數(shù)之間關(guān)系的一般規(guī)律； （3）求回歸方程； （4）如果某天的氣溫是2℃，預測這天賣出的熱飲杯數(shù)。 解： （4）當x=2時，y=143.063 反思總結(jié)，當堂檢測。 1、求樣本數(shù)據(jù)的線性回歸方程，可按下列步驟進行： （1）計算平均數(shù)，； （2）求a，b； （3）寫出回歸直線方程。 2、回歸方程被樣本數(shù)據(jù)惟一確定，對同一個總體，不同的樣本數(shù)據(jù)對應不同的回歸直線，所以回歸直線也具有隨機性.。 3、對于任意一組樣本數(shù)據(jù)，利用上述公式都可以求得“回歸方程”，如果這組數(shù)據(jù)不具線性相關(guān)關(guān)系，即不存在回歸直線，那么所得的“回歸方程”是沒有實際意義的。因此，對一組樣本數(shù)據(jù)，應先作散點圖，在具有線性相關(guān)關(guān)系的前提下再求回歸方程