《精編【課堂坐標(biāo)】高中數(shù)學(xué)北師大版必修一學(xué)業(yè)分層測(cè)評(píng):第二章 函數(shù)7 Word版含解析》由會(huì)員分享��,可在線閱讀���,更多相關(guān)《精編【課堂坐標(biāo)】高中數(shù)學(xué)北師大版必修一學(xué)業(yè)分層測(cè)評(píng):第二章 函數(shù)7 Word版含解析(5頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1���、精編北師大版數(shù)學(xué)資料
學(xué)業(yè)分層測(cè)評(píng)(七)
(建議用時(shí):45分鐘)
[學(xué)業(yè)達(dá)標(biāo)]
一、選擇題
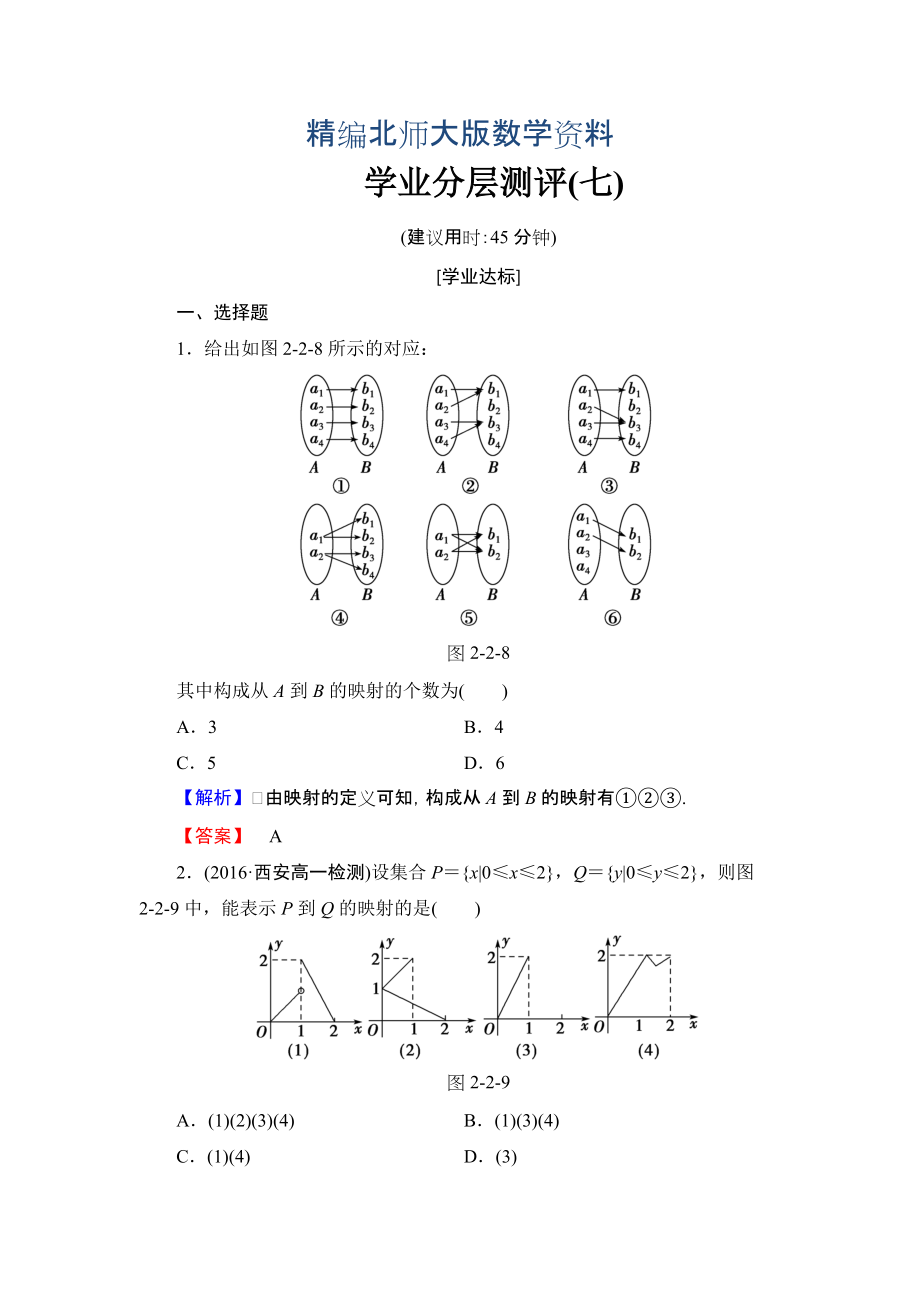
1.給出如圖228所示的對(duì)應(yīng):
圖228
其中構(gòu)成從A到B的映射的個(gè)數(shù)為( )
A.3 B.4
C.5 D.6
【解析】 由映射的定義可知��,構(gòu)成從A到B的映射有①②③.
【答案】 A
2.(2016·西安高一檢測(cè))設(shè)集合P={x|0≤x≤2}����,Q={y|0≤y≤2}�����,則圖229中����,能表示P到Q的映射的是( )
圖229
A.(1)(2)(3)
2����、(4) B.(1)(3)(4)
C.(1)(4) D.(3)
【解析】 如圖(1),對(duì)于P中的每個(gè)元素x在Q中都有唯一的像�,所以它是P到Q的映射;在圖(2)中�,當(dāng)P中元素x取(0,1]的值時(shí),在Q中對(duì)應(yīng)的元素不唯一����,所以(2)不是映射;在圖(3)中�����,當(dāng)P的元素取(1,2]的值時(shí)�����,Q中沒(méi)有元素與它對(duì)應(yīng)�����,所以(3)不是P到Q的映射����;與(1)相同,(4)也是P到Q的映射.
【答案】 C
3.下列對(duì)應(yīng)法則中����,能建立從集合A={1,2,3,4,5}到集合B={0,3,8,15,24}的映射的是( )
A.f:x→x2-x B.f:x→x+(x-1)2
C.f:x→x2+1 D.f:x→x2
3、-1
【解析】 因?yàn)?2-1=0,22-1=3,32-1=8,42-1=15,52-1=24.
故從集合A到集合B的映射的對(duì)應(yīng)關(guān)系為f:x→x2-1.
【答案】 D
4.已知A=B=R�,x∈A,y∈B�����,f:x→y=ax+b是從A到B的映射�,若1和8的原像分別是3和10,則5在f下的像是( )
A.3 B.4
C.5 D.6
【解析】 由題意解得
∴f:x→y=x-2���,
∴5在f下的像是5-2=3.
【答案】 A
5.已知映射f:A→B�����,其中集合A={-3�����,-2��,-1,1,2,3,4}�,集合B中的元素都是A中的元素在映射f下的像,且對(duì)任意的a∈A�����,在B中和它對(duì)應(yīng)的元素是|
4�、a|,則集合B中的元素的個(gè)數(shù)是( )
A.4 B.5
C.6 D.7
【解析】 對(duì)應(yīng)關(guān)系是f:a→|a|.因此�,3和-3對(duì)應(yīng)的像是3;-2和2對(duì)應(yīng)的像是2�����;1和-1對(duì)應(yīng)的像是1�;4對(duì)應(yīng)的像是4.所以B={1,2,3,4}.故選A.
【答案】 A
二、填空題
6.設(shè)M=N=R�,f:x→-x2+2x是M到N的映射�,若對(duì)于N中元素p���,在M中恰有一個(gè)原像,則p的值為_(kāi)_______.
【解析】 由題意知����,關(guān)于x的方程-x2+2x=p有兩相等實(shí)根,∴Δ=4-4p=0��,p=1.
【答案】 1
7.下列對(duì)應(yīng)f是從集合A到集合B的函數(shù)的是________.
①A={1,2,
5�、3},B={7,8,9}��,f(1)=f(2)=7�����,f(3)=8�;
②A=Z,B={-1,1}�,n為奇數(shù)時(shí),f(n)=-1�����;n為偶數(shù)時(shí),f(n)=1�����;
③A={高一一班的男生}���,B={男生的身高}�,對(duì)應(yīng)關(guān)系f��;每個(gè)男生對(duì)應(yīng)自己的身高.
【解析】 對(duì)于①��,集合A中的元素沒(méi)有剩余��,即A中的任何一個(gè)元素在B中都有唯一確定的像�,同時(shí)集合A和B都是數(shù)集,可知對(duì)應(yīng)f是集合A到集合B的函數(shù).
同理�����,對(duì)于②�����,對(duì)應(yīng)f也是集合A到集合B的函數(shù).
對(duì)于③�����,集合A,B不是數(shù)集�,不是函數(shù)關(guān)系.
【答案】?���、佗?
8.已知集合A=B=R,映射f:x→x2+2x-4�,若a在B中且在A中沒(méi)有原像,則a的取值范圍是_
6����、_______.
【解析】 ∵x2+2x-4=(x+1)2-5≥-5.
∵a在B中且在A中沒(méi)有原像,
則a<-5.
【答案】 (-∞�����,-5)
三���、解答題
9.設(shè)集合P=Q={(x����,y)|x����,y∈R}�����,從集合P到集合Q的映射為f:(x�,y)→(x+y���,xy)��,求
(1)集合Q中與集合P中元素(3,2)對(duì)應(yīng)的元素�;
(2)集合P中與集合Q中元素(3,2)對(duì)應(yīng)的元素.
【解】 (1)由3+2=5,3×2=6����,
故與集合P中元素對(duì)應(yīng)的元素為(5,6).
(2)由解得或
故與集合Q中元素(3,2)對(duì)應(yīng)的元素為(1,2)或(2,1).
10.下列對(duì)應(yīng)是否是從A到B
7、的映射��,能否構(gòu)成函數(shù)�?
(1)A=R,B=R���,f:x→y=����;
(2)A={0,1,2,9},B={0,1,4,9,64}�,
f:a→b=(a-1)2.
(3)A=[0,+∞)�����,B=R���,f:x→y2=x;
(4)A={x|x是平面M內(nèi)的矩形}�,B={x|x是平面M內(nèi)的圓},f:作矩形的外接圓.
【解】 (1)當(dāng)x=-1時(shí)���,y的值不存在��;
∴不是映射�����,更不是函數(shù).
(2)在f的作用下�����,A中的0,1,2,9分別對(duì)應(yīng)到B中的1,0,1,64��,∴是映射���,也是函數(shù).
(3)∵當(dāng)A中的元素不為零時(shí)�,B中有兩個(gè)元素與之對(duì)應(yīng)�,∴不是映射,更不是函數(shù).
(4)是映射����,但不是函數(shù),因?yàn)锳�、B不是
8、數(shù)集.
[能力提升]
1.設(shè)集合A與集合B都是自然數(shù)集N���,映射f:A→B把集合A中的元素n映射到集合B中為元素n2+n��,則在映射f下��,像20的原像是( )
A.2 B.3
C.4 D.4或-5
【解析】 令n2+n=20��,即n2+n-20=0����,
解得n=-5或4.
∵n∈N,∴n=4.
【答案】 C
2.集合A={a����,b},B={-1,0,1}��,從A到B的映射f:A→B滿(mǎn)足f(a)+f(b)=0��,那么這樣的映射f:A→B的個(gè)數(shù)有( )
A.2個(gè) B.3個(gè)
C.5個(gè) D.8個(gè)
【解析】 由f(a)�,f(b)∈{-1,0,1},且f(a)+f(b)=0知���,這樣的映射有:
9�����、
共3個(gè).
【答案】 B
3.給定映射f(x,y)→(�����,x+y)�,在對(duì)應(yīng)關(guān)系f下像(2,3)的原像是(a,b)�,則函數(shù)y=ax2+bx的頂點(diǎn)坐標(biāo)是________.
【解析】 由題意a=4,b=-1,則y=4x2-x的頂點(diǎn)坐標(biāo)為.
【答案】
4.設(shè)集合A=B={(x�,y)|x,y∈R}���,f是A到B的一個(gè)映射���,并滿(mǎn)足f:(x,y)→(-xy���,x-y).
(1)求B中元素(3�,-4)在A中的原像���;
(2)試探索B中哪些元素在A中存在原像��;
(3) 求B中元素(a���,b)在A中有且只有一個(gè)原像時(shí),a�����,b所滿(mǎn)足的關(guān)系式.
【導(dǎo)學(xué)號(hào):04100023】
【解】 (1)設(shè)(x���,y)是B中元素(3�,-4)在A中的原像,于是解得或
所以(3���,-4)在A中的原像有兩個(gè)����,即(-1,3)和(-3,1).
(2)設(shè)任意(a���,b)∈B���,則它在A中的原像(x,y)應(yīng)滿(mǎn)足,
由②式得y=x-b,將它代入①式���,并化簡(jiǎn)得x2-bx+a=0.③
當(dāng)且僅當(dāng)Δ=b2-4a≥0時(shí)���,方程③有實(shí)數(shù)根,因此只有當(dāng)B中元素(a����,b)滿(mǎn)足b2-4a≥0時(shí)�����,在A中才有原像.
(3)由以上(2)的解題過(guò)程可知���,當(dāng)B中元素(a,b)滿(mǎn)足b2=4a時(shí)���,它在A中有且只有一個(gè)原像.
 精編【課堂坐標(biāo)】高中數(shù)學(xué)北師大版必修一學(xué)業(yè)分層測(cè)評(píng):第二章 函數(shù)7 Word版含解析
精編【課堂坐標(biāo)】高中數(shù)學(xué)北師大版必修一學(xué)業(yè)分層測(cè)評(píng):第二章 函數(shù)7 Word版含解析