《2018年中考數(shù)學(xué)復(fù)習(xí) 第5單元 四邊形 第23課時(shí) 多邊形與平行四邊形檢測(cè) 湘教版》由會(huì)員分享����,可在線閱讀,更多相關(guān)《2018年中考數(shù)學(xué)復(fù)習(xí) 第5單元 四邊形 第23課時(shí) 多邊形與平行四邊形檢測(cè) 湘教版(5頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�����。
1����、
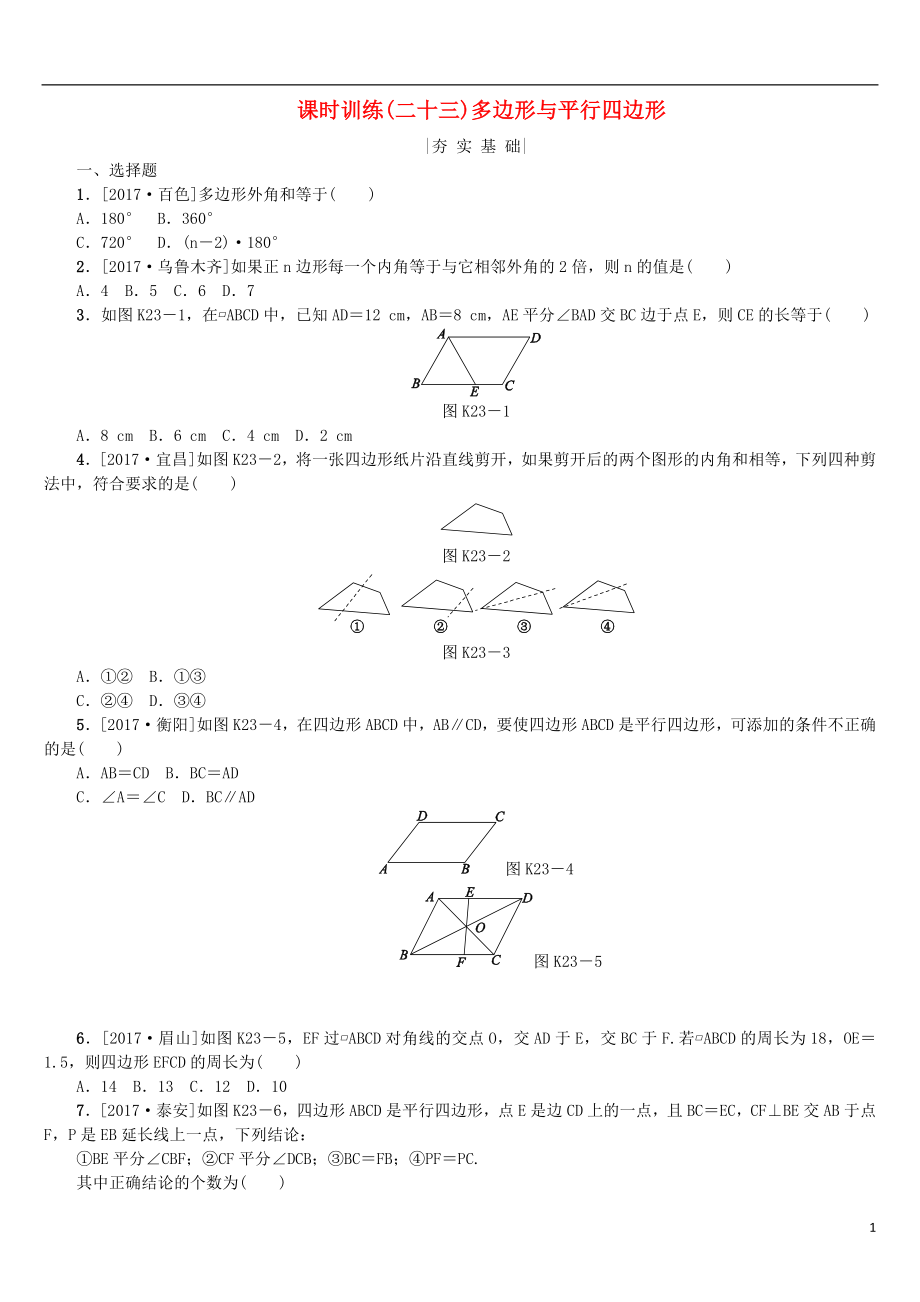
課時(shí)訓(xùn)練(二十三)多邊形與平行四邊形
|夯 實(shí) 基 礎(chǔ)|
一、選擇題
1.[2017·百色]多邊形外角和等于( )
A.180° B.360°
C.720° D.(n-2)·180°
2.[2017·烏魯木齊]如果正n邊形每一個(gè)內(nèi)角等于與它相鄰?fù)饨堑?倍���,則n的值是( )
A.4 B.5 C.6 D.7
3.如圖K23-1���,在?ABCD中,已知AD=12 cm��,AB=8 cm����,AE平分∠BAD交BC邊于點(diǎn)E�����,則CE的長等于( )
圖K23-1
A.8 cm B.6 cm C.4 cm D.2 cm
4.[2017·宜昌]如圖K23-2,將一張
2����、四邊形紙片沿直線剪開,如果剪開后的兩個(gè)圖形的內(nèi)角和相等����,下列四種剪法中,符合要求的是( )
圖K23-2
圖K23-3
A.①② B.①③
C.②④ D.③④
5.[2017·衡陽]如圖K23-4��,在四邊形ABCD中��,AB∥CD��,要使四邊形ABCD是平行四邊形��,可添加的條件不正確的是( )
A.AB=CD B.BC=AD
C.∠A=∠C D.BC∥AD
圖K23-4
圖K23-5
6.[2017·眉山]如圖K23-5���,EF過?ABCD對(duì)角線的交點(diǎn)O����,交AD于E,交BC于F.若?ABCD的周長為18�����,OE=1.5���,則四邊形EFCD的周長為(
3�、 )
A.14 B.13 C.12 D.10
7.[2017·泰安]如圖K23-6�,四邊形ABCD是平行四邊形,點(diǎn)E是邊CD上的一點(diǎn)�,且BC=EC,CF⊥BE交AB于點(diǎn)F����,P是EB延長線上一點(diǎn),下列結(jié)論:
①BE平分∠CBF��;②CF平分∠DCB�����;③BC=FB;④PF=PC.
其中正確結(jié)論的個(gè)數(shù)為( )
圖K23-6
A.1 B.2 C.3 D.4
二��、填空題
8.[2017·揚(yáng)州]在?ABCD中�,∠B+∠D=200°,則∠A=________°.
9.[2017·邵陽]如圖K23-7所示的正六邊形ABCDEF����,連接FD,則∠FDC的大小為____
4�、____.
圖K23-7
10.[2017·懷化]如圖K23-8�,在平行四邊形ABCD中,對(duì)角線AC����,BD相交于點(diǎn)O,點(diǎn)E是AB的中點(diǎn)���,OE=5 cm���,則AD的長為________ cm.
圖K23-8
11.[2017·南京]如圖K23-9,∠1是五邊形ABCDE的一個(gè)外角���,若∠1=65°�,則∠A+∠B+∠C+∠D=________.
圖K23-9
圖K23-10
12.[2017·西寧]如圖K23-10�,將平行四邊形ABCD沿EF對(duì)折��,使點(diǎn)A落在點(diǎn)C處�,若∠A=60°����,AD=4,AB=6���,則AE的長為________.
三�、解答題
13.[2017
5���、·烏魯木齊]如圖K23-11�,四邊形ABCD是平行四邊形�,E,F(xiàn)是對(duì)角線BD上的兩點(diǎn)�����,且BF=ED���,求證:AE∥CF.
圖K23-11
14.[2017·湘潭]如圖K23-12��,在平行四邊形ABCD中���,DE=CE����,連接AE并延長交BC的延長線于點(diǎn)F.
(1)求證:△ADE≌△FCE���;
(2)若AB=2BC�����,∠F=36°,求∠B的度數(shù).
圖K23-12
15.[2017·鎮(zhèn)江]如圖K23-13�����,點(diǎn)B����、E分別在AC、DF上���,AF分別交BD���、CE于點(diǎn)M��、N��,∠A=∠F����,∠1=∠2.
(1)求證:四邊形BCED是平行四邊形���;
(2)已知DE=2����,連接BN.若BN
6�、平分∠DBC,求CN的長.
圖K23-13
|拓 展 提 升|
圖K23-14
16.[2017·呼和浩特]如圖K23-14���,在平行四邊形ABCD中�,∠B=30°�,AB=AC,O是兩條對(duì)角線的交點(diǎn)�����,過點(diǎn)O作AC的垂線分別交邊AD,BC于點(diǎn)E���,F(xiàn)����;點(diǎn)M是邊AB的一個(gè)三等分點(diǎn)��,則△AOE與△BMF的面積比為________.
17.[2017·德陽]如圖K23-15����,在平行四邊形ABCD中,E�、F分別是AB、BC的中點(diǎn)�,CE⊥AB,垂足為E����,AF⊥BC�,垂足為F,AF與CE相交于點(diǎn)G.
(1)證明:△CFG≌△AEG.
(2)若AB=4����,求四邊形AGCD的對(duì)角線GD的長.
7�、
圖K23-15
參考答案
1.B [解析] 所有多邊形的外角和都是360°.
2.C [解析] 設(shè)正多邊形的每個(gè)外角為x°��,則相鄰的內(nèi)角為2x°�����,根據(jù)“外角與相鄰的內(nèi)角互補(bǔ)”�����,得x+2x=180�,解得x=60,根據(jù)多邊形的外角和是360°��,得n==6.
3.C
4.B [解析] 根據(jù)剪開所得圖形的內(nèi)角和進(jìn)行識(shí)別與判斷��,第1個(gè)剪開所得兩個(gè)圖形都是四邊形����,符合要求;第2個(gè)剪開所得兩個(gè)圖形分別是五邊形和三角形�,不符合要求;第3個(gè)剪開所得兩個(gè)圖形都是三角形�,符合要求;第4個(gè)剪開所得兩個(gè)圖形分別是三角形和四邊形���,不符合要求.
5.B [解析] 添加B��,具備“一組對(duì)邊平行���,另一組對(duì)
8�����、邊相等”的條件�����,不能推斷為平行四邊形�����,B錯(cuò)誤����,故選B.
6.C [解析] 因?yàn)樗倪呅蜛BCD是平行四邊形����,所以AD∥BC��,OA=OC,所以∠OAE=∠OCF�����,又因?yàn)椤螦OE=∠COF�,所以△AOE≌△COF,所以AE=CF��,OE=OF���,而AB=CD��,AD=BC��,所以四邊形EFCD的周長為AD+CD+EF=×18+2×1.5=12.
7.D [解析] ∵AB∥CD�����,∴∠ABE=∠BEC.
∵CE=CB�����,∴∠CBE=∠BEC.
∴∠CBE=∠ABE.即BE平分∠ABC.故①正確�����;∵CE=CB�,CF⊥BE,
∴CF平分∠DCB.故②正確�;
∵AB∥CD,∴∠DCF=∠CFB.
∵∠DC
9���、F=∠FCB�,∴∠BCF=∠CFB���,
∴BC=BF.故③正確.
∵BF=CB����,CF⊥BE��,∴BE垂直平分CF�����,
∵PF=PC.故④正確.
8.80 [解析] 根據(jù)“平行四邊形的對(duì)角相等���、鄰角互補(bǔ)”可以求得∠A=180°-200°÷2=80°.
9.90° [解析] 三角形EFD是等腰三角形����,且頂角為正六邊形的內(nèi)角�,為120°,所以∠FDE=30°�����,所以∠FDC=120°-30°=90°.
10.10
11.425° [解析] 根據(jù)多邊形內(nèi)角和公式得(5-2)×180°=540°��,∵∠1=65°�����,∴∠AED=115°���,
∴∠A+∠B+∠C+∠D=540°-115°=425°.
10�、12. [解析] 過點(diǎn)C作CH⊥AB交AB的延長線于H�����,∵四邊形ABCD為平行四邊形�,∠A=60°,∴∠ABC=120°���,∴∠CBH=60°��,又BC=4�����,∴BH=2���,CH=2 ��,則AH=8��,在Rt△ECH中��,設(shè)AE=CE=a�,則EH=8-a�,∵CH2+EH2=CE2,∴(2 )2+(8-a)2=a2����,解得:a=,即AE=.
13.證明:∵四邊形ABCD是平行四邊形����,
∴AD∥BC,且AD=BC,∴∠ADE=∠CBF.
又∵BF=ED�,∴△AED≌△CFB(SAS),
∴∠AED=∠CFB���,∴AE∥CF.
14.解:(1)證明:∵四邊形ABCD是平行四邊形,
∴AD=BC�����,AD∥
11�、BC,∴∠DAE=∠EFC.
在△ADE和△FCE中�,
∴△ADE≌△FCE(AAS).
(2)由(1)得AD=FC,
又∵AD=BC�,∴FC=BC,
∴BF=FC+BC=2BC�����,
∵AB=2BC�,∴AB=BF,
∴∠F=∠FAB=36°�����,
由三角形的內(nèi)角和為180°得,∠B=180°-∠F-∠FAB=180°-36°-36°=108°.
15.解:(1)證明:∵∠A=∠F�,∴DF∥AC.
又∵∠1=∠2,∠1=∠DMF�,
∴∠DMF=∠2.∴DB∥EC.
∵DB∥EC,DF∥AC�,
∴四邊形BCED為平行四邊形.
(2)∵BN平分∠DBC,∴∠DBN=∠NBC��,
12����、
∵DB∥EC,∴∠DBN=∠BNC���,
∴∠NBC=∠BNC��,∴BC=CN.
∵四邊形BCED為平行四邊形�,
∴BC=DE=2.∴CN=2.
16.3∶4 [解析] 連接MF�����,過點(diǎn)M作MP⊥BC交BC于點(diǎn)P�,過點(diǎn)A作AQ⊥BC交BC于點(diǎn)Q,在平行四邊形ABCD中�,O是兩條對(duì)角線的交點(diǎn)����,
∴△AOE≌△COF���,又∵∠B=30°��,AB=AC�����,
∴∠ACF=∠B=30°,∵AC⊥EF�,
∴在Rt△OFC中,設(shè)OF=x����,則OC=x,F(xiàn)C=2x���,∴S△AOE=S△OFC=OF×OC=x2��,易知AB=AC=2OC=2 x.
在Rt△ABQ中��,BQ=3x���,∴BC=6x�,∴BF=4x�,∵點(diǎn)M是
13、邊AB的一個(gè)三等分點(diǎn)�,
∴MB=x,在Rt△BMP中����,MP=MB=x,∴S△BMF=BF×MP=x2�����,
∴S△AOE∶S△BMF=3∶4.
17.解:(1)證明:∵E是AB的中點(diǎn)����,CE⊥AB,
∴CA=CB.
∵F是BC的中點(diǎn)��,且AF⊥BC��,∴AB=AC=BC����,∴AE=CF��,
在△CFG和△AEG中����,
∴△CFG≌△AEG.
(2)連接GD�����,由(1)知�,△ABC為等邊三角形,從而△CAD也為等邊三角形�����,∵AF⊥BC�,
∴∠GAC=∠EAF=30°����,
而AE=AB=2,
∴在Rt△AGE中�,AG===,
∵∠GAD=∠GAC+∠CAD=90°�,∴在Rt△ADG中,
根據(jù)勾股定理得GD2=AG2+AD2��,
即GD2=()2+42=,∴GD=.
5
 2018年中考數(shù)學(xué)復(fù)習(xí) 第5單元 四邊形 第23課時(shí) 多邊形與平行四邊形檢測(cè) 湘教版
2018年中考數(shù)學(xué)復(fù)習(xí) 第5單元 四邊形 第23課時(shí) 多邊形與平行四邊形檢測(cè) 湘教版