《2018年秋九年級數(shù)學(xué)上冊 第4章 相似三角形 4.7 圖形的位似練習(xí) （新版）浙教版》由會員分享，可在線閱讀，更多相關(guān)《2018年秋九年級數(shù)學(xué)上冊 第4章 相似三角形 4.7 圖形的位似練習(xí) （新版）浙教版（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。

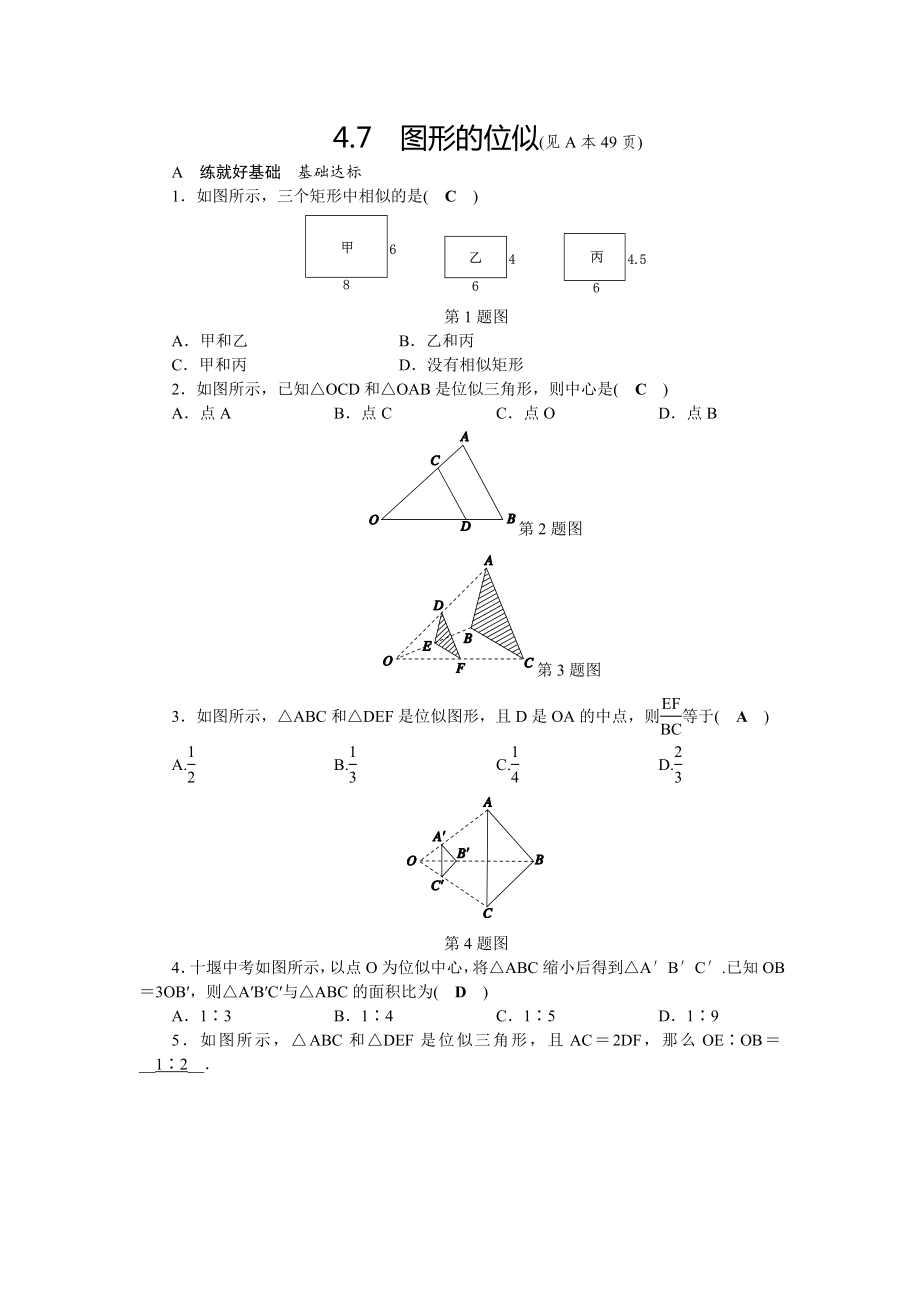
1、4.7　圖形的位似(見A本49頁) A　練就好基礎(chǔ)　基礎(chǔ)達(dá)標(biāo) 1．如圖所示，三個矩形中相似的是(　C　) 第1題圖 A．甲和乙 B．乙和丙 C．甲和丙 D．沒有相似矩形 2．如圖所示，已知△OCD和△OAB是位似三角形，則中心是(　C　) A．點(diǎn)A　 B．點(diǎn)C　 C．點(diǎn)O　 D．點(diǎn)B 第2題圖 　　第3題圖 3．如圖所示，△ABC和△DEF是位似圖形，且D是OA的中點(diǎn)，則等于(　A　) A. B. C. D. 第4題圖 4．十堰中考如圖所示，以點(diǎn)O為位似中心，將△ABC縮小后得到△A′B′

2、C′.已知OB＝3OB′，則△A′B′C′與△ABC的面積比為(　D　) A．1∶3 B．1∶4 C．1∶5 D．1∶9 5．如圖所示，△ABC和△DEF是位似三角形，且AC＝2DF，那么OE∶OB＝__1∶2__． 第5題圖 　　第6題圖 6．2017·蘭州中考如圖所示，四邊形ABCD與四邊形EFGH相似，位似中心點(diǎn)是O，＝，則＝____． 7．2017·濱州中考在平面直角坐標(biāo)系中，點(diǎn)C，D的坐標(biāo)分別為C(2，3)，D(1，0)，現(xiàn)以原點(diǎn)為位似中心，將線段CD放大得到線段AB.若點(diǎn)D的對應(yīng)點(diǎn)B在x軸上且OB＝2，則點(diǎn)C的對應(yīng)點(diǎn)A的坐標(biāo)為　(4，6)或(－4，

3、－6)?。? 8．如圖所示，四邊形ABCD各頂點(diǎn)的坐標(biāo)分別為A(2，6)，B(4，2)，C(6，2)，D(6，4)，在第一象限內(nèi)，畫出以原點(diǎn)為位似中心，相似比為1∶2的位似圖形A1B1C1D1，并寫出各點(diǎn)坐標(biāo)． 第8題圖 解：如圖可知：A1(1，3)，B1(2，1)，C1(3，1)，D1(3，2)． 第8題答圖 9．如圖所示，方格紙中每個小正方形的邊長為1，△ABC和△DEF的頂點(diǎn)都在方格紙的格點(diǎn)上． 第9題圖 (1)判斷△ABC和△DEF是否相似； (2)P1，P2，P3，P4，P5，D，F(xiàn)是△DEF邊上的7個格點(diǎn)，請在這7個格點(diǎn)中選取3個點(diǎn)作為三角形的頂點(diǎn)，使

4、構(gòu)成的三角形與△ABC相似(要求寫出所有符合條件的三角形，并在圖中連結(jié)相應(yīng)線段，不必證明)； (3)在(2)中所找的三角形中，其中是否存在與△EP2P4成位似的三角形？如果存在，請寫出位似比，并在圖中確定位似中心． 解：(1)根據(jù)勾股定理，得AB＝2，AC＝，BC＝5； DE＝4，DF＝2， EF＝2， ∵＝＝＝＝， ∴△ABC∽△DEF. 第9題答圖 (2)答案不唯一，下面6個三角形中的任意1個均可． △P2P5D，△P4P5F，△P2P4D， △P4P5D，△P2P4P5，△P1FD. (3)存在. △EP2P4與△P2P4P5，位似比為1∶1，位似中心為P2P4

5、的中點(diǎn)． B　更上一層樓　能力提升 10．如圖所示，其中屬于位似圖形的有(　C　) 第10題圖 A．1個 B．2個 C．3個　 D．4個 第11題圖 11．2017·遂寧中考如圖所示，直線y＝x＋1與x軸，y軸分別交于A，B兩點(diǎn)，△BOC與△B′O′C′是以點(diǎn)A為位似中心的位似圖形，且相似比為1∶2，則點(diǎn)B′的坐標(biāo)為　(3，2)或(－9，－2)?。? 第12題圖 12．鹽城中考如果兩個一次函數(shù)y＝k1x＋b1和y＝k2x＋b2滿足k1＝k2，b1≠b2，那么稱這兩個函數(shù)為“平行一次函數(shù)”．如圖所示，已知函數(shù)y＝－2x＋4的圖象與x軸、y軸分別交于A，B兩

6、點(diǎn)，一次函數(shù)y＝kx＋b與y＝－2x＋4是“平行一次函數(shù)”． (1)若函數(shù)y＝kx＋b的圖象過點(diǎn)(3，1)，求b的值； (2)若函數(shù)y＝kx＋b的圖象與兩坐標(biāo)軸圍成的三角形和△AOB構(gòu)成位似圖形，位似中心為原點(diǎn)，位似比為1∶2，求函數(shù)y＝kx＋b的表達(dá)式． 解：(1)由已知，得k＝－2，把點(diǎn)(3，1)和k＝－2代入y＝kx＋b中，得1＝－2×3＋b，∴b＝7. (2)根據(jù)位似比為1∶2得函數(shù)y＝kx＋b的圖象有兩種情況： ①不經(jīng)過第三象限時，過(1，0)和(0，2)，這時表達(dá)式為y＝－2x＋2； ②不經(jīng)過第一象限時，過(－1，0)和(0，－2)，這時表達(dá)式為y＝－2x－2. C　

7、開拓新思路　拓展創(chuàng)新 13．學(xué)了本節(jié)課，以下四位同學(xué)談了自己的學(xué)習(xí)體會． 小剛說：位似圖形必是相似圖形． 小明說：相似圖形必是位似圖形． 小麗說：兩個位似圖形的位似比與相似比的意義相同． 小慧說：兩個位似圖形的位似比與相似比相等． 請你根據(jù)自己的認(rèn)識對這四位同學(xué)的觀點(diǎn)做出判斷與解釋． 解：小剛的說法是正確的；小明的說法不正確，由位似的定義可得；小麗的說法不正確， 因為由位似比與相似比的定義可得它們的意義是不同的；小慧的說法是正確的． 第14題圖 14．如圖所示，用下面的方法可以畫△AOB的內(nèi)接等邊三角形，閱讀后證明相應(yīng)問題． 畫法：①在△AOB內(nèi)畫等邊△CDE，使

8、點(diǎn)C在OA上，點(diǎn)D在OB上． ②連結(jié)OE并延長，交AB于點(diǎn)E′，過點(diǎn)E′作E′C′∥EC，交OA于點(diǎn)C′，作E′D′∥ED，交OB于點(diǎn)D′. ③連結(jié)C′D′，則△C′D′E′是△AOB的內(nèi)接三角形． 求證：△C′D′E′是等邊三角形． 證明：∵E′C′∥EC，E′D′∥ED， ∴△OCE∽△OC′E′，△ODE∽△OD′E′， ∴CE∶C′E′＝OE∶OE′，DE∶D′E′＝OE∶OE′， ∠CEO＝∠C′E′O，∠DEO＝∠D′E′O， ∴CE∶C′E′＝DE∶D′E′，∠CED＝∠C′E′D′， ∴△CDE∽△C′D′E′. ∵△CDE是等邊三角形， ∴△C′D′E′也是等邊三角形.