《浙江省2018年中考數(shù)學(xué)總復(fù)習(xí) 第五章 基本圖形(二)第26講 三視圖與展開圖講解篇》由會(huì)員分享,可在線閱讀�,更多相關(guān)《浙江省2018年中考數(shù)學(xué)總復(fù)習(xí) 第五章 基本圖形(二)第26講 三視圖與展開圖講解篇(9頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1�、
第26講 三視圖與展開圖
1.三視圖
考試內(nèi)容
考試
要求
三視圖
正視圖
從正面得到的,由前向后觀察物體的視圖叫做正視圖�,正視圖反映物體的長和高.
b
左視圖
從側(cè)面得到的,由左向右觀察物體的視圖叫做左視圖�,左視圖反映物體的寬和高.
俯視圖
從水平面得到的,由上向下觀察物體的視圖叫做俯視圖�,俯視圖反映物體的長和寬.
畫物體
的三視
圖
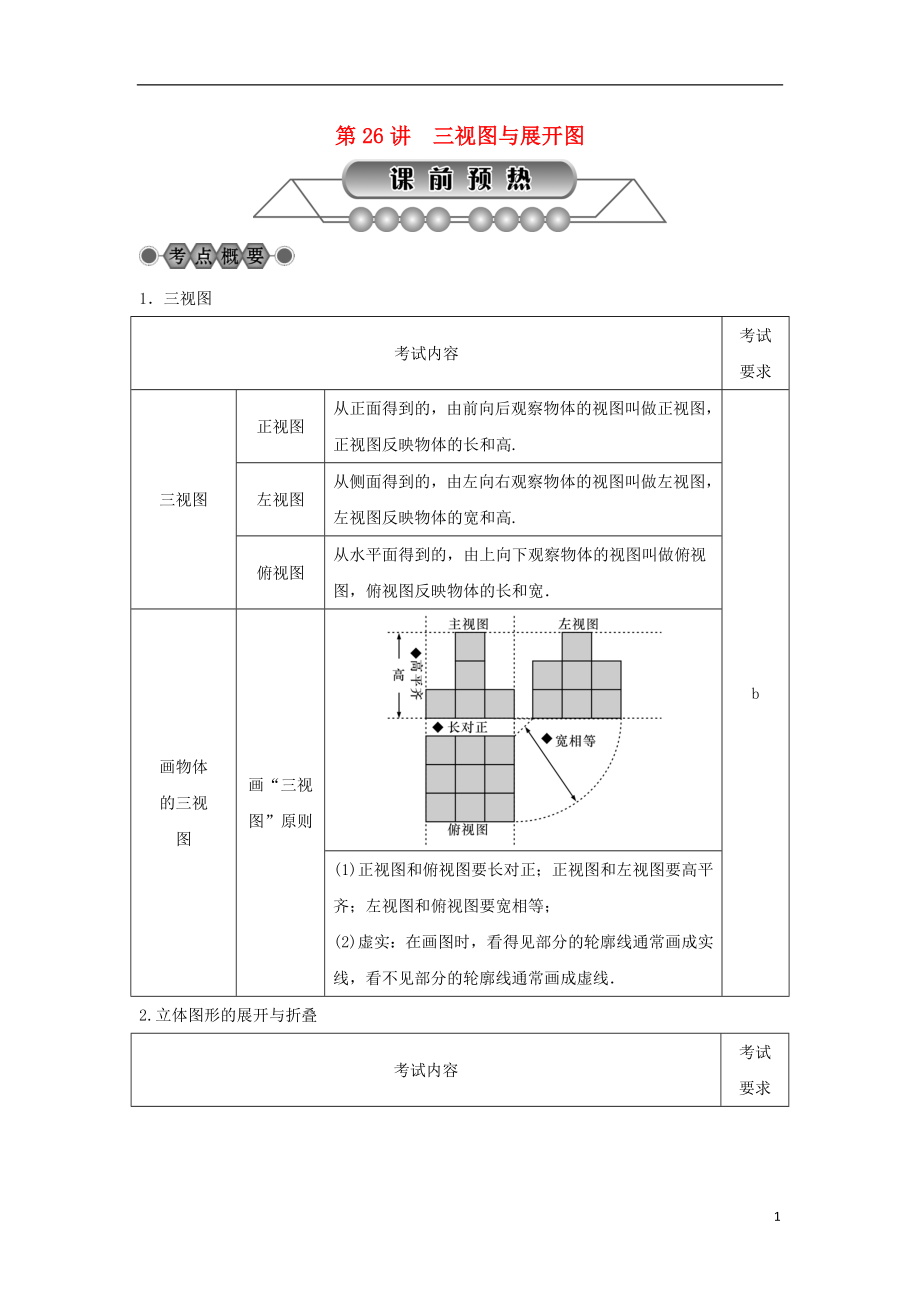
畫“三視圖”原則
(1)正視圖和俯視圖要長對(duì)正;正視圖和左視圖要高平齊�;左視圖和俯視圖要寬相等;
(2)虛實(shí):在畫圖時(shí)�,看得見部分的輪廓線通常畫成實(shí)線,看不見部分的輪廓線通常畫成虛線.
2.立體圖形的展
2�、開與折疊
考試內(nèi)容
考試
要求
圓錐的
側(cè)面展
開圖
圓錐的側(cè)面是一個(gè)扇形�,能根據(jù)展開圖想象和制作立體模型.
b
直棱柱
側(cè)面展
開圖
直棱柱側(cè)面展開圖是矩形,能根據(jù)展開圖想象和制作立體模型.
正方體
的平面
展開圖
一個(gè)立體圖形沿不同的棱剪開就得到不同的平面圖形.
考試內(nèi)容
考試
要求
基本
思想
轉(zhuǎn)化思想�,將立體圖形轉(zhuǎn)化為平面圖形,如物體的包裝等.
b
1.(2017·衢州)如圖是由四個(gè)相同的小立方體搭成的幾何體�,它的主視圖是( )
第1題圖 第2題圖
2.(201
3、7·麗水)如圖是底面為正方形的長方體�,下面有關(guān)它的三個(gè)視圖的說法正確的是( )
A.俯視圖與主視圖相同 B.左視圖與主視圖相同
C.左視圖與俯視圖相同 D.三個(gè)視圖都相同
3.(2017·寧波)如圖所示的幾何體的俯視圖為( )
4.(2017·金華)一個(gè)幾何體的三視圖如圖所示�,這個(gè)幾何體是( )
A.球 B.圓柱 C.圓錐 D.立方體
【問題】如圖�,下列四個(gè)幾何體是水平放置.
(1)這四個(gè)幾何體中,主視圖與其他三個(gè)不相同的是________�;
4、(2)圖(1)的直三棱柱�,底面是邊長為2的正三角形,高為4�,則此直三棱柱的側(cè)面展開圖的面積________;
(3)圖(2)的圓柱�,底面半徑為2,高為4�,則此圓柱左視圖的面積________;
(4)通過(1)(2)(3)的解答�,請(qǐng)你聯(lián)想三視圖和立體圖形展開圖的相關(guān)知識(shí)、方法.
【歸納】通過開放式問題�,歸納、疏理簡(jiǎn)單幾何體的三視圖�、展開圖.
類型一 判斷(畫)幾何體的三視圖
下列幾何體中,俯視圖相同的是( )
A.①② B.①③ C.②③ D.②④
【解后感悟】掌握從不同方向看物體的方法
5�、和畫幾何體三視圖的要求,通過仔細(xì)觀察�、比較、分析�,可選出正確答案.
1. (1)(2016·湖州)由六個(gè)相同的立方體搭成的幾何體如圖所示,則它的主視圖是( )
(2)(2017·黔西南州)下列四個(gè)幾何體中,主視圖與左視圖相同的幾何體有( )
A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè)
(3) (2017·臺(tái)州)如圖所示的工件是由兩個(gè)長方體構(gòu)成的組合體�,則它的主視圖是( )
類型二 由三視圖判斷原幾何體的形狀
(2016·黃石)某幾何體的主視圖和左視圖如圖所示,則該幾何體可能是(
6�、 )
A.長方體 B.圓錐 C.圓柱 D.球
【解后感悟】由三視圖確定幾何體,往往需要把三個(gè)視圖組合起來�、空間想象綜合考慮;掌握常見幾何體的三視圖是解題的關(guān)鍵.
2. (1)(2015·桂林)下列四個(gè)物體的俯視圖與如圖給出視圖一致的是( )
(2) (2017·嘉興模擬)如圖是某個(gè)幾何體的三視圖�,該幾何體是( )
A.長方體 B.正方體 C.圓柱 D.三棱柱
(3)(2015·隨州)如圖是一個(gè)長方體的三視圖(單位:
7、cm)�,根據(jù)圖中數(shù)據(jù)計(jì)算這個(gè)長方體的體積是 cm3.
類型三 立體圖形的展開與折疊
如圖給定的是紙盒的外表面,下面能由它折疊而成的是( )
【解后感悟】常見幾何體的展開與折疊:①棱柱的平面展開圖是由兩個(gè)相同的多邊形和一些長方形組成�,按棱柱表面不同的棱剪開,可能得到不同組合方式的平面展開圖�,特別關(guān)注正方體的表面展開圖;②圓柱的平面展開圖是由兩個(gè)相同的圓形和一個(gè)長方形組成的�;③圓錐的平面展開圖是由一個(gè)圓形和一個(gè)扇形組成的.
3. (1)(2017·漳州模擬)如圖是一個(gè)長方體包裝盒,則它的平面展開圖是( )
(2)(2015·廣州)如圖是一個(gè)
8�、幾何體的三視圖,則該幾何體的展開圖可以是( )
(3)如圖1是邊長為1的六個(gè)小正方形組成的圖形�,它可以圍成圖2的正方體,則圖1中小正方形頂點(diǎn)A�,B在圍成的正方體上的距離是( )
A.0 B.1 C. D.
(4)(2016·十堰)如圖,從一張腰長為60cm�,頂角為120°的等腰三角形鐵皮OAB中剪出一個(gè)最大的扇形OCD�,用此剪下的扇形鐵皮圍成一個(gè)圓錐的側(cè)面(不計(jì)損耗),則該圓錐的高為( )
A.10cm B.15cm
9、 C.10cm D.20cm
類型四 幾何體的綜合運(yùn)用
學(xué)校食堂廚房的桌子上整齊地?cái)[放著若干相同規(guī)格的碟子�,碟子的個(gè)數(shù)與碟子的高度的關(guān)系如下表:
碟子的個(gè)數(shù)
碟子的高度(單位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
(1)當(dāng)桌子上放有x(個(gè))碟子時(shí),請(qǐng)寫出此時(shí)碟子的高度(用含x的式子表示)�;
(2)分別從三個(gè)方向上看,其三視圖如上圖所示�,廚房師傅想把它們整齊疊成一摞,求疊成一摞后的高度.
【解后感悟】從問題中獲取信息(讀表)�,找出碟子個(gè)數(shù)與碟子高度之間的關(guān)系式是解此題的關(guān)鍵
10、.
4. (1)(2017·湖州)如圖是按1∶10的比例畫出的一個(gè)幾何體的三視圖�,則該幾何體的側(cè)面積是( )
A.200cm2
B.600cm2
C.100πcm2
D.200πcm2
(2) 如圖,圓柱形容器高為18cm�,底面周長為24cm,在杯內(nèi)壁離杯底4cm的點(diǎn)B處有一滴蜂蜜�,此時(shí)一只螞蟻正好在杯外壁,離杯上沿2cm與蜂蜜相對(duì)的點(diǎn)A處�,則螞蟻從外壁A處到達(dá)內(nèi)壁B處的最短距離為 cm.
【課本改變題】教材母題--浙教版九下第76頁例題
如圖是某幾何體的三視圖,則該幾何體的體積是( )
A.18 B.
11�、54 C.108 D.216
【方法與對(duì)策】由三視圖求原幾何體的體積,正確恢復(fù)原幾何體是解決問題的關(guān)鍵.這類題是中考熱點(diǎn)題型�,平時(shí)學(xué)習(xí)中也要注意平面圖形和空間圖形的轉(zhuǎn)化.
【分不清三視圖中的實(shí)線與虛線】
一個(gè)空心的圓柱如圖所示,那么它的主視圖是( )
參考答案
第26講 三視圖與展開圖
【考題體驗(yàn)】
1.D 2.B 3.D 4.B
【知識(shí)引擎】
【解析】(1)圖(1)的主視圖為長方形�;圖(2)的主視圖為長方形;圖(3)的主視圖為長方形�;圖(4)的主視圖為三角形.故主視圖與其他三個(gè)不相同的是圖(4). (2
12、)側(cè)面展開圖是矩形�,側(cè)面積為6×4=24. (3)左視圖的面積為4×4=16. (4)畫三視圖�,根據(jù)三視圖描述簡(jiǎn)單幾何體�,直棱柱,圓錐側(cè)面展開圖等
【例題精析】
例1?、冖鄣母┮晥D都是圓,有圓心�,故選C.
例2 ∵如圖所示幾何體的主視圖和左視圖分別是長方形和圓,∴該幾何體可能是圓柱體.故選C.
例3 B
例4 (1)2+1.5(x-1)=(1.5x+0.5)cm (2)由三視圖可知共有12個(gè)碟子�,∴疊成一摞的高度=1.5×12+0.5=18.5(cm).
【變式拓展】
1.(1)A (2)D (3)A 2.(1)C (2)D (3)24 3.(1)A (2)A (3)B (4)D 4.(1)D (2)20
【熱點(diǎn)題型】
【分析與解】由三視圖可看出:該幾何體是一個(gè)正六棱柱,其中底面正六邊形的邊長為6�,高是2,所以該幾何體的體積=6××62×2=108.故選C.
【錯(cuò)誤警示】A
9
 浙江省2018年中考數(shù)學(xué)總復(fù)習(xí) 第五章 基本圖形(二)第26講 三視圖與展開圖講解篇
浙江省2018年中考數(shù)學(xué)總復(fù)習(xí) 第五章 基本圖形(二)第26講 三視圖與展開圖講解篇