《浙江省2018年中考數(shù)學總復習 第一章 數(shù)與式 第4講 分式及其運算講解篇》由會員分享�,可在線閱讀,更多相關《浙江省2018年中考數(shù)學總復習 第一章 數(shù)與式 第4講 分式及其運算講解篇(9頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1����、
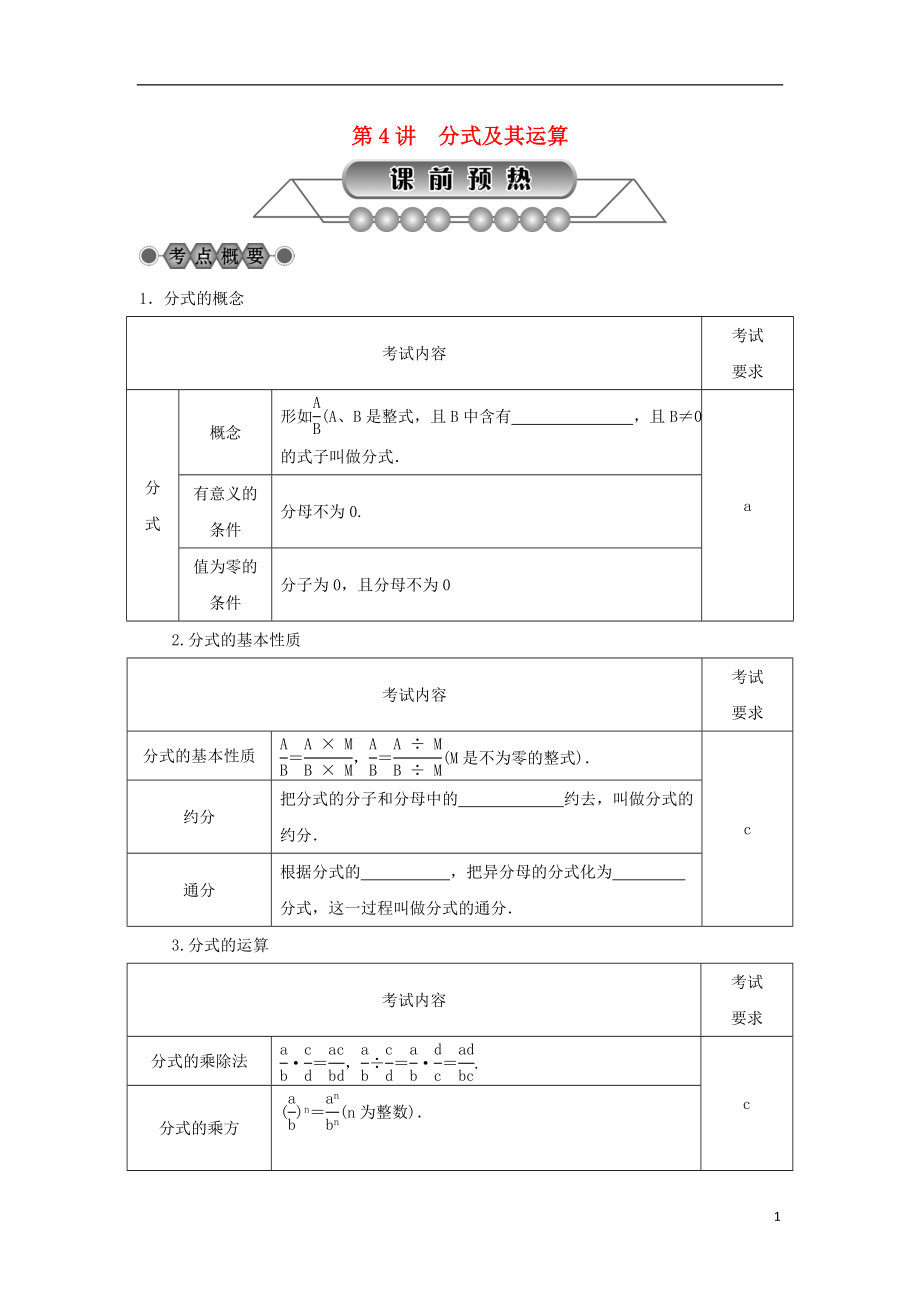
第4講 分式及其運算
1.分式的概念
考試內(nèi)容
考試
要求
分
式
概念
形如(A、B是整式����,且B中含有 �,且B≠0)的式子叫做分式.
a
有意義的條件
分母不為0.
值為零的條件
分子為0����,且分母不為0
2.分式的基本性質(zhì)
考試內(nèi)容
考試
要求
分式的基本性質(zhì)
=,=(M是不為零的整式).
c
約分
把分式的分子和分母中的 約去��,叫做分式的約分.
通分
根據(jù)分式的 �,把異分母的分式化為
分式��,這一過程叫做分式的通分.
3.分式的運算
考試
2����、內(nèi)容
考試
要求
分式的乘除法
·=,÷=·=.
c
分式的乘方
()n=(n為整數(shù)).
分式的加減法
±=��,±=.
分式的混合運算
在分式的混合運算中����,應先算乘方,再將除法化為乘法�,進行約分化簡,最后進行加減運算.遇到有括號����,先算括號里面的.
考試內(nèi)容
考試
要求
基本
方法
1.乘方時一定要先確定乘方結(jié)果的符號�����,負數(shù)的偶次方為正����,負數(shù)的奇次方為負.
c
2.在分式的加減運算中��,如需要通分時�,一定要先把分母可以分解因式的多項式分解因式后再找最簡公分母,分式的乘除運算中����,需要約分時,也要先把可以分解因式的多項式分解因式再約分.
3.分式求值:
3�、可根據(jù)所給條件和求值式的特征進行適當?shù)淖冃巍⑥D(zhuǎn)化和溝通.主要有以下技巧:①整體代入法�;②參數(shù)法;③平方法�����;④代入法��;⑤倒數(shù)法.
1.(2015·麗水)分式-可變形為( )
A.- B. C.- D.
2.(2016·臺州)化簡的結(jié)果是( )
A.-1 B.1 C. D.
3.(2017·湖州)要使分式有意義,x的取值應滿足__________________
4���、____________.
4.(2017·舟山)若分式的值為0����,則x的值為____________________.
5.(2015·湖州)計算:-.
【問題】(1)從三個代數(shù)式:①a2-2ab+b2��,②3a-3b�����,③a2-b2中任意選擇兩個代數(shù)式構(gòu)造成分式����,然后進行化簡�,并求當a=6,b=3時該分式的值.
(2)通過對(1)的解答���,你能想到與分式相關的哪些信息.
【歸納】通過開放式問題�����,歸納�、疏理分式概念,以及分式相關的性質(zhì)����,探究分式化簡方法.
類型一 分式的概念
分式.
(1)若分式有意義,則x的取值范圍是________�����;
5�����、
(2)若分式的值為0�����,則x的值為________�;
(3)把分式化為最簡分式________.
【解后感悟】分式有意義,首先求出使分母等于0的字母的值��,然后讓未知數(shù)不等于這些值���,便可使分式有意義���;分式的值為0的條件是:首先求出使分子為0的字母的值�����,再檢驗這個字母的值是否使分母的值為0�,當它使分母的值不為0時�����,這就是所要求的字母的值�����;化為最簡分式是分母�、分子因式分解,再約分.
1.已知分式����,若分式無意義��,則x的取值范圍是____________________���;若分式的值為零�,則x=____________________.
2.(2016·濱州)下列分式中����,最簡分式是( )
6�����、
A. B. C. D.
類型二 分式的約分和通分
計算:(1)(2016·淄博)=________����;
(2)+=________���;
(3)-=________���;
(4)1-a-=________.
【解后感悟】分式化簡關鍵是約分,約分的關鍵是找公因式��,若分子和分母有多項式���,先將其因式分解��,然后將相同的因式約去即可.分式的加減運算關鍵是通分���,通分的關鍵是找最簡公分母.
3.(1)(2016·麗水)+的運算結(jié)果正確的
7、是( )
A. B. C. D.a(chǎn)+b
(2)(2015·紹興)化簡+的結(jié)果是( )
A.x+1 B. C.x-1 D.
(3)若a����、b都是正實數(shù)����,且-=����,則=____________________.
(4)(2016·荊州)當a=+1,b=-1時�����,代數(shù)式的值是 .
(5)(2015·臺州)先化簡�,再求值:-,其中a=-1.
類型三 分式的運算與求值
(1)(2016·內(nèi)江)化簡:÷=___
8�����、_____.
(2)(2015·黃岡)化簡:÷=________.
(3)(2015·衢州)先化簡���,再求值:(x2-9)÷,其中x=-1.
(4)先化簡���,再求值:÷�����,其中x滿足x2+x-2=0.
【解后感悟】(1)解決這類題關鍵是把握好通分與約分.分式加減的本質(zhì)是通分�����,乘除的本質(zhì)是約分.(2)熟知分式混合運算的法則是解答此題的關鍵.化簡求值題要將原式化為最簡后再代值����,從求出x的兩個數(shù)中選一個數(shù)代入求值,但要注意分式成立的條件.
4.(2015·成都)化簡:(+)÷.
5.先化簡����,再求值:÷+1,在0�����,1���,2�,三個數(shù)中選
9�、一個合適的,代入求值.
類型四 與分式有關的變形和應用
觀察下列等式:
第1個等式:a1==×(1-);
第2個等式:a2==×(-)�����;
第3個等式:a3==×(-)���;
第4個等式:a4==×(-)�;
…
請解答下列問題:
(1)按以上規(guī)律列出第5個等式:a5=______=______��;
(2)用含有n的代數(shù)式表示第n個等式:an=________=________(n為正整數(shù))��;
(3)求a1+a2+a3+a4+…+a100的值.
【解后感悟】本題是數(shù)字變化規(guī)律��,要求首先分析題意����,通過觀察、分
10�、類歸納、抽象出數(shù)列的規(guī)律�����,并進行推導得出答案.
6.(1)如圖���,設k=(a>b>0)����,則有( )
A.k>2
B.1<k<2
C.<k<1
D.0<k<
(2)一種商品原來的銷售利潤率是47%.現(xiàn)在由于進價提高了5%�,而售價沒變,所以該商品的銷售利潤率變成了____________________%.【注:銷售利潤率=(售價-進價)÷進價】.
【探索規(guī)律題】
(2015·巴中)a是不為1的數(shù)����,我們把稱為a的差倒數(shù),如:2的差倒數(shù)為=-1����;-1的差倒數(shù)是=;已知a1=-���,a2是a1的差倒數(shù)����,a3是a2的差倒數(shù).a(chǎn)4是a3的差倒數(shù)�,…依此類推,則a20
11��、15=________.
【方法與對策】此題是找規(guī)律的題目��,對于找規(guī)律的題目首先應找出哪些部分發(fā)生了變化,是按照什么規(guī)律變化的���,找出規(guī)律是解題的關鍵�����,該題型是中考的熱點.
【分式的分母不能為零�����,除數(shù)不能為零】
分式的值是0��,則x的值為________.
參考答案
第4講 分式及其運算
【考點概要】
1.字母 2.公因式 基本性質(zhì) 同分母
【考題體驗】
1.D 2.D 3.x≠2 4.2 5.a+b.
【知識引擎】
【解析】(1)答案不唯一.選?�、?、②得==����,當a=6,b=3時��,原式==1(有6種情況). (2)分式概念�、運算法則,注
12����、意點等.
【例題精析】
例1 (1)x≠±3���;(2)無解��;(3). 例2 (1)1-2a��;(2)1��;(3)����;(4) 例3 (1)a;(2)���;(3)原式=(x+3)(x-3)·=x(x+3)=x2+3x����,當x=-1時�,原式=(-1)2+3×(-1)=-2;(4)原式=·=·=.由x2+x-2=0����,解得x1=-2����,x2=1��,∵x≠1��,∴當x=-2時�����,原式==. 例4 (1)�����,×(-)��;
(2)�,×(-).(3)a1+a2+a3+a4+…+a100=×(1-)+×(-)+×(-)+…+×(-)=×=×=×=.
【變式拓展】
1. x=2 -2
2. A
3. (1)C (2)A (3)- (4) (5)�,.
4. .
5. .當x=1時,原式=.
6.(1)B (2)40
【熱點題型】
【分析與解】a1=-��,a2是a1的差倒數(shù)���,即a2==���,a3是a2的差倒數(shù)��,即a3==3�,a4是a3的差倒數(shù)�,即a4==-,…依此類推��,∵2015÷3=671……2����,∴a2015=a2=.故答案為:.
【錯誤警示】
當=0時��,x2-4=0且x2-x-2≠0��,∴x=-2.故答案為-2.
9
 浙江省2018年中考數(shù)學總復習 第一章 數(shù)與式 第4講 分式及其運算講解篇
浙江省2018年中考數(shù)學總復習 第一章 數(shù)與式 第4講 分式及其運算講解篇