《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計 第二板塊 熱點(diǎn)問題突破 專題4 歸納與猜想專題提升演練 新人教版》由會員分享，可在線閱讀，更多相關(guān)《2019年中考數(shù)學(xué)總復(fù)習(xí)優(yōu)化設(shè)計 第二板塊 熱點(diǎn)問題突破 專題4 歸納與猜想專題提升演練 新人教版（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

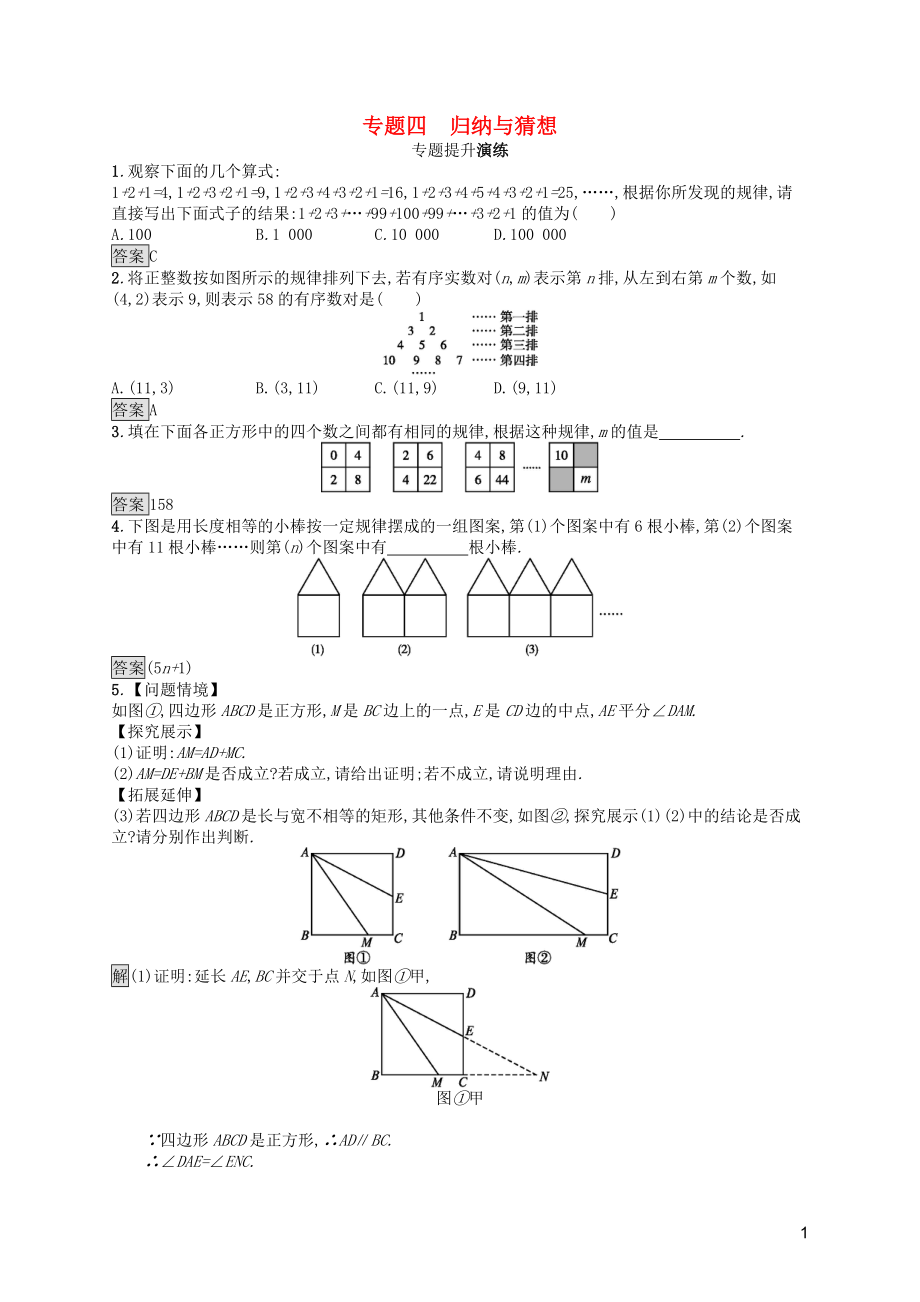
1、專題四　歸納與猜想 專題提升演練 1.觀察下面的幾個算式: 1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,……,根據(jù)你所發(fā)現(xiàn)的規(guī)律,請直接寫出下面式子的結(jié)果:1+2+3+…+99+100+99+…+3+2+1的值為(　　) A.100 B.1 000 C.10 000 D.100 000 答案C 2.將正整數(shù)按如圖所示的規(guī)律排列下去,若有序?qū)崝?shù)對(n,m)表示第n排,從左到右第m個數(shù),如(4,2)表示9,則表示58的有序數(shù)對是(　　) A.(11,3) B.(3,11) C.(11,9) D.(9,11)

2、 答案A 3.填在下面各正方形中的四個數(shù)之間都有相同的規(guī)律,根據(jù)這種規(guī)律,m的值是　　　　　.? 答案158 4.下圖是用長度相等的小棒按一定規(guī)律擺成的一組圖案,第(1)個圖案中有6根小棒,第(2)個圖案中有11根小棒……則第(n)個圖案中有　　　　　根小棒.? 答案(5n+1) 5.【問題情境】 如圖①,四邊形ABCD是正方形,M是BC邊上的一點(diǎn),E是CD邊的中點(diǎn),AE平分∠DAM. 【探究展示】 (1)證明:AM=AD+MC. (2)AM=DE+BM是否成立?若成立,請給出證明;若不成立,請說明理由. 【拓展延伸】 (3)若四邊形ABCD是長與寬不相等的矩形,

3、其他條件不變,如圖②,探究展示(1)(2)中的結(jié)論是否成立?請分別作出判斷. 解(1)證明:延長AE,BC并交于點(diǎn)N,如圖①甲, 圖①甲 ∵四邊形ABCD是正方形,∴AD∥BC. ∴∠DAE=∠ENC. ∵AE平分∠DAM,∴∠DAE=∠MAE. ∴∠ENC=∠MAE.∴MA=MN. 在△ADE和△NCE中,∠DAE=∠CNE,∠AED=∠NEC,DE=CE, ∴△ADE≌△NCE(AAS). ∴AD=NC. ∴MA=MN=NC+MC=AD+MC. (2)AM=DE+BM成立. 證明:過點(diǎn)A作AF⊥AE,交CB的延長線于點(diǎn)F, 如圖①乙所示. 圖①乙

4、 ∵四邊形ABCD是正方形, ∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC. ∵AF⊥AE,∴∠FAE=90°. ∴∠FAB=90°-∠BAE=∠DAE. 在△ABF和△ADE中,∠FAB=∠EAD,AB=AD,∠ABF=∠D=90°, ∴△ABF≌△ADE(ASA). ∴BF=DE,∠F=∠AED. ∵AB∥DC,∴∠AED=∠BAE. ∵∠FAB=∠EAD=∠EAM, ∴∠AED=∠BAE=∠BAM+∠EAM =∠BAM+∠FAB=∠FAM. ∴∠F=∠FAM.∴AM=FM. ∴AM=FB+BM=DE+BM. (3)①結(jié)論AM=AD+MC仍然成

5、立. 證明:延長AE,BC并交于點(diǎn)P,如圖②甲. 圖②甲 ∵四邊形ABCD是矩形,∴AD∥BC. ∴∠DAE=∠EPC. ∵AE平分∠DAM, ∴∠DAE=∠MAE. ∴∠EPC=∠MAE.∴MA=MP. 在△ADE和△PCE中,∠DAE=∠CPE,∠AED=∠PEC,DE=CE, ∴△ADE≌△PCE(AAS).∴AD=PC. ∴MA=MP=PC+MC=AD+MC. ②結(jié)論AM=DE+BM不成立. 證明:假設(shè)AM=DE+BM成立. 過點(diǎn)A作AQ⊥AE,交CB的延長線于點(diǎn)Q, 如圖②乙所示. 圖②乙 ∵四邊形ABCD是矩形, ∴∠BAD=∠D=

6、∠ABC=90°,AB∥DC. ∵AQ⊥AE,∴∠QAE=90°. ∴∠QAB=90°-∠BAE=∠DAE. ∴∠Q=90°-∠QAB=90°-∠DAE=∠AED. ∵AB∥DC,∴∠AED=∠BAE. ∵∠QAB=∠DAE=∠EAM, ∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠QAB=∠QAM. ∴∠Q=∠QAM.∴AM=QM. ∴AM=QB+BM. ∵AM=DE+BM,∴QB=DE. 在△ABQ和△ADE中,∠QAB=∠EAD,∠ABQ=∠D=90°,BQ=DE, ∴△ABQ≌△ADE(AAS).∴AB=AD. 與條件“AB≠AD”矛盾,故假設(shè)不成立. ∴AM=DE+BM不成立. 3